TABLE OF CONTENTS
The formal definition of a definite integral is
stated in terms of the limit of a Riemann sum. Riemann sums are covered
in the calculus lectures and in the textbook. For simplicity's sake, we
will use a more informal definiton for a definite integral. We will
introduce the definite integral defined in terms of area.
Let f(x) be a continuous function on the interval
[a,b]. Consider the area bounded by the curve, the x-axis and the lines
x=a and x=b.
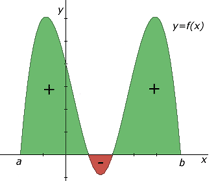
The area of the region that lies above the x-axis should be treated as
a positive (+) value, while the area of the region that lies below the
x-axis should be treated as a negative (-) value.
The image below illustrates this concept. The
positive area, above the x-axis, is shaded green and labelled "+",
while the negative area, below the x-axis, is shaded red and labelled
"-".
The integral of the function f(x) from a
to b is equal to the sum of the individual areas bounded by the
function, the x-axis and the lines x=a and x=b. This integral is
denoted by
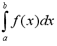
where f(x) is called the integrand, a is
the lower limit and b is the upper limit. This type of integral is
called a definite integral. When evaluated, a definite integral
results in a real number. It is independent of the choice of sample
points (x, f(x)).
Properties of Definite Integrals
The following properties are helpful when
calculating definite integrals.
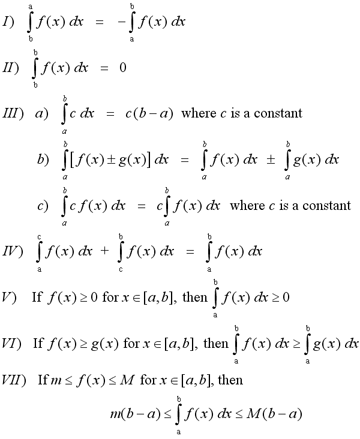
Examples
1
| Evaluate the integral by finding the area beneath the curve
The Fundamental Theorem of Calculus defines the
relationship between the processes of differentiation and integration.
That relationship is that differentiation and integration are inverse
processes.
The Fundamental Theorem of Calculus : Part 1
If f is a continuous function on [a,b], then the
function denoted by
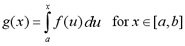
is continuous on [a,b], differentiable on (a,b)
and g'(x) = f(x).
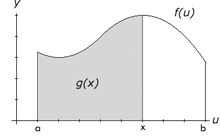
If f(t) is continuous on [a,b], the function g(x)
that's equal to the the area bounded by the u-axis and the function
f(u) and the lines u=a and u=x will be continuous on [a,b] and
differentiable on (a,b). Most importantly, when we differentiate the
function g(x), we will find that it is equal to f(x). The graph to the
right illustrates the function f(u) and the area g(x).
The Fundamental Theorem of Calculus : Part 2
If f is a continuous function on [a,b], then
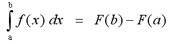
where F is any antiderivative of f.
If f is continuous on [a,b], the definite
integral with integrand f(x) and limits a and b is simply equal to the
value of the antiderivative
F(x) at b minus the value of F at a. This property allows us to easily
solve definite integrals, if we can find the antiderivative function of
the integrand.
Parts one and two of the Fundamental Theorem of
Calculus can be combined and simplified into one theorem.
The Fundamental Theorem of Calculus
Let f be a continuous function on [a,b].
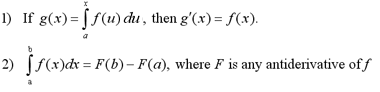
An indefinite integral has the form
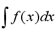
When evaluated, an indefinite integral results in
a function (or family of functions). An indefinite integral of a
function f(x) is also known as the antiderivative of f. A
function F is an antiderivative of f on an interval I, if F'(x) = f(x)
for all x in I. This is a strong indication that that the processes of
integration and differentiation are interconnected.
The following tables list the formulas for
antidifferentiation. These formulas allow us to determine the function
that results from an indefinite integral. Since the formulas are for
the most general indefinite integral, we add a constant C to each one.
With these formulas and the Fundamental Theorem of Calculus, we can
evaluate simple definite integrals.
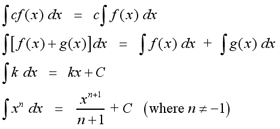
The next table lists indefinite integrals
involving trigonometric functions.
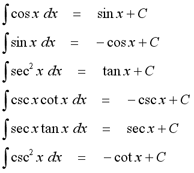
Note: After finding an
indefinite integral, you can always check to see if your answer is
correct. Since integration and differentiation are inverse processes,
you can simply differentiate the function that results from
integration, and see if it is equal to the integrand.
Examples
2
| Find the general indefinite integrals
3
| Evaluate the definite integral
4
| Evaluate the definite integral of the absolute value of a function
The total change theorem is an adaptation of the
second part of the Fundamental Theorem of Calculus. The Total
Change Theorem states: the integral of a rate of change is equal to
the total change.
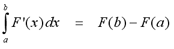
If we know that the function f(x) is the
derivative of some function F(x), then the definite integral of f(x)
from a to b is equal to the change in the function F(x) from a to b.
Examples
5
| Given the velocity function, find the displacement during a period of
time
Suppose that we have an integral such as
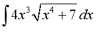
With our current knowledge of integration, we
can't find the general equation of this indefinite integral. There are
no antidifferentiation formulas for this type of integral. However,
from our knowledge of differentiation, specifically the
chain rule, we
know that 4x3 is the derivative of the function within the
square root, x4 + 7. We must also account for the chain rule
when we are performing integration. To do this, we use the substitution
rule.
The Substitution Rule states: if u = g(x)
is a differentiable function and f is continuous on the range of g,
then
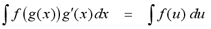
Note: Recall that if u
= g(x), then du = g'(x)dx. If we substitute u into the left side of the
equation for g(x) and du for g'(x)dx, then we get the integral on the
right side of the equation.
From our previous example, if we let u = (x4+7),
then du = 4x3dx. If we substitutite these values into the
integral, we get an integral that can be solved using the
antidifferentiation formulas.
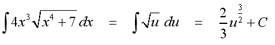
However, this answer is still in terms of u. We
must substitute u = (x4+7) into the resulting function, so
that it is a function of x, rather than u.
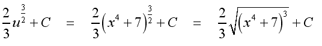
The substitution rule also applies to definite
integrals. The Substitution Rule for Definite Integrals states:
If f is continuous on the range of u = g(x) and g'(x) is continuous on
[a,b], then
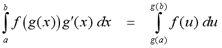
Examples
6
| Find the general indefinite integrals using the substitution rule
7
| Evaluate the definite integral using the substitution rule
If f(x) is continuous on [-a, a] and f is an even function, then
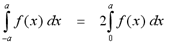
If f(x) is continuous on [-a, a] and f is an odd function, then
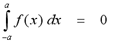
These properties of integrals of symmetric
functions are very helpful when solving integration problems. Some of
the more challenging problems can be solved quite simply by using this
property.
Examples
8
| Evaluate the definite integral of the symmetric function
Suppose that we have an integral such as
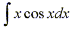
Similar to integrals solved using the substitution method, there are no
general equations for this indefinite integral. However there do not appear to be
any clear substitutions that could be made to simplify this integral. This brings
us to an integration technique known as integration by parts, which will call upon
our knowledge of the Product Rule for differentiation.
The Product
Rule states: If f and g are differentiable functions,
then
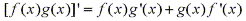
By taking the indefinite integral of both sides of the equation we have:
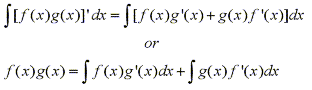
and we can rearrange this equation as
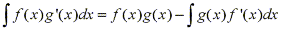
To make it easier to remember it is commonly written in the following
notation. Let u=f(x) and v=g(x). Then the differentiables are du=f'(x)dx and
dv=g'(x)dx, so by the substitution rule, the formula for integration by parts becomes:
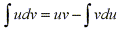
From our previous example, if we let u=x and dv=cosx, then du=dx and v=sinx.
If we substitute these values into the formula we have:
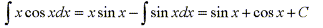
Note: By choosing u=x we obtain a simpler integral
than we started with. Had we chose u=cosx and dv=x then du=-sinx and v=(1/2)x2
so integration by parts gives:
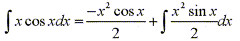
This equation is correct, but the integral is more difficult
than the one we started with.
When choosing u and dv always try to choose u=f(x) to be a function that
becomes simpler when differentiated (or at least not more complicated) and to choose
dv=g'(x) to be a function that can be easily integrated to give v.
Examples
9
| Find the general indefinite integral by integration by parts
10 | Evaluate the definite integral by integration by parts
Suppose we have an integral such as
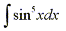
The easy mistake is to simply make the substitution
u=sinx, but then du=cosxdx. So in order to integrate powers of sine we
need an extra cosx factor. Similarily, in order to integrate powers of cosine
we need an extra sinx factor. Thus for this example knowing we need an extra
sinx factor to integrate powers of cosine we can separate one sine factor and
convert the remaining sin4x to an expression involving cosine using the
identity sin2x + cos2x = 1.
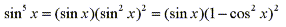
Now by using our knowledge of substitution we can evaluate the integral
by letting u=cosx, then du=-sinxdx and
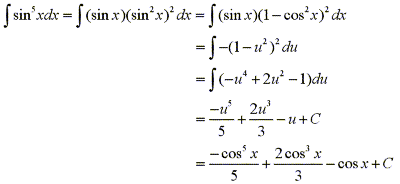
Now consider the integral
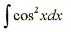
If we were to use the method from the previous example and separate one
cosine factor we would be left with a factor of cosine of odd degree which isn't
easily converted to sine. We must now consider the half angle formulas
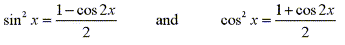
Using the half angle formula for cos2x, we have:
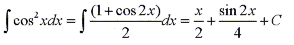
Strategy for Evaluating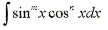
- (a)
- If the power of sine is odd (m=2k+1), save one sine factor and use the identity
sin2x + cos2x = 1 to convert the remaining factors in terms of cosine.
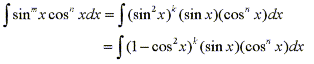
then substitute u=cosx.-
- (b)
- If the power of cosine is odd (n=2k+1), save one cosine factor and use the
identity sin2x + cos2x = 1 to convert the remaining factors in terms
of sine.
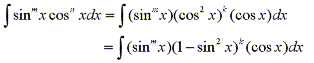
then substitute u=sinx.-
- (c)
-
- If the powers of both sine and cosine are even then use the half angle
identities.
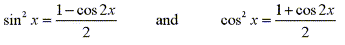
In some cases it may be helpful to use the identity
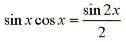
-
11
| Find the indefinite trigonometric integral
12
| Using the half angle formulas solve the indefinite trigonometric integral
13
| Find the definite trigonometric integral
Now that we have learned strategies for solving integrals with factors
of sine and cosine we can use similar techniques to solve integrals with factors
of tangent and secant. Using the identity sec2x = 1 + tan2x
we are able to convert even powers of secant to tangent and vice versa. Now we will
consider two examples to illustrate two common strategies used to solve integrals of
the form
Suppose we have an integral such as
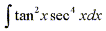
Observing that (d/dx)tanx=sec2x we can separate a factor of
sec2x and still be left with an even power of secant. Using the identity
sec2x = 1 + tan2x we can convert the remaining sec2x
to an expression involving tangent. Thus we have:
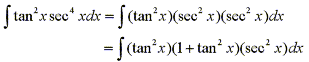
Then substitute u=tanx to obtain:
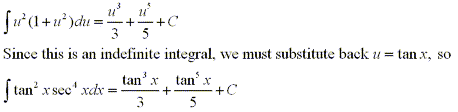
Note: Suppose we tried to use the substitution
u=secx, then du=secxtanxdx. When we separate out a factor of secxtanx we are left with
an odd power of tangent which is not easily converted to secant.
Consider the integral
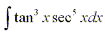
Since (d/dx)secx=secxtanx we can separate a factor of secxtanx and still be
left with an even power of tangent which we can easily convert to an expression
involving secant using the identity sec2x = 1 + tan2x.
Thus we have:
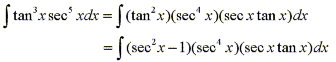
Then substitute u=secx to obtain:
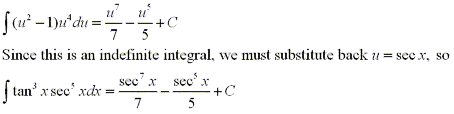
Note: Suppose we tried to use the substitution
u=tanx, then du=sec2xdx. When we separate out a factor of sec2x
we are left with an odd power of secant which is not easily converted to tangent.
Strategy for Evaluating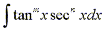
- (a)
- If the power of secant is even (n=2k, k>2) save a factor of
sec2x and use the identity sec2x = 1 + tan2x to express
the remaining factors in terms of tanx.
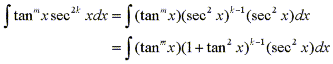
then substitute u=tanx.-
- (b)
- If the power of tangent is odd (m=2k+1), save a factor of secxtanx and use
the identity sec2x = 1 + tan2x to express the remaining factors in
terms of secx.

then substitute u=secx.-
Note: If the power of secant is even and the power
of tangent is odd then either method will suffice, although there may be less work
involved to use method (a) if the power of secant is smaller, and method (b) if the power
of tangent is smaller.
14
| Find the indefinite trigonometric integral
15 | Find the definite trigonometric integral
Integrals of cotangent and cosecant are very similar to those with tangent
and secant.
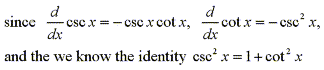
it is easy to see that integrals of the form
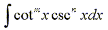 can be solved by nearly identical methods
as are integrals of the form can be solved by nearly identical methods
as are integrals of the form 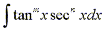 . .
16 | Find the indefinite trigonometric integral
Unlike integrals with factors of both tangent and secant, integrals that have
factors of only tangent, or only secant do not have a general strategy for solving. Use
of trig identities, substitution and integration by parts are all commonly used to solve
such integrals. For example,

If we make the substitution u=secx, then du=secxtanxdx, and we are left with
the simple integral
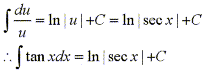
Similarily we can use the same technique to solve
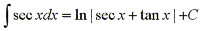
17
| Find the definite trigonometric integral
18
| Find the definite trigonometric integral
19
| Find the indefinite trigonometric integral
Another problem that may be encountered when solving trigonometric integrals
are integrals of the form
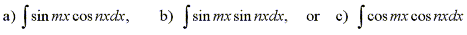
Using the product formulas which are deduced from the
addition/subtraction rules we have the corresponding identities
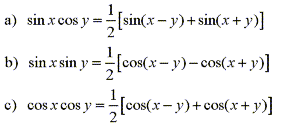
20
| Find the indefinite trigonometric integral using the product formulas
Sometimes trigonometric substitutions are very effective even when at first it
may not be so clear why such a substitution be made. For example, when finding the area
of a circle or an ellipse you may have to find an integral of the form
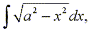 where a>0. where a>0.
It is difficult to make a substitution where the new variable is a function of
the old one, (for example, had we made the substitution u = a2 - x2,
then du= -2xdx, and we are unable to cancel out the -2x.) So we must consider a change in
variables where the old variable is a function of the new one. This is where trigonometric
identities are put to use. Suppose we change the variable from x to
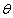 by making the substitution x = a
sin θ.
Then using the trig identity by making the substitution x = a
sin θ.
Then using the trig identity 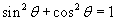 we can simplify the integral
by eliminating the root sign. we can simplify the integral
by eliminating the root sign.
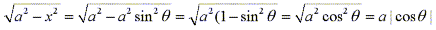
By changing x to a function with a different variable we are essentially using
the The Substitution Rule in reverse. If
x=g(t) then by restricting the boundaries on g we can assure that g has an inverse function;
that is, g is one-to-one. In the example above we would require
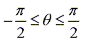 to assure to assure 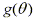 has
an inverse function. has
an inverse function.
If we look at the Substitution Rule and replace u with x and x with t, we obtain
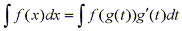
This is known as the "inverse substitution".

Integration of rational functions by partial fractions is a fairly simple
integrating technique used to simplify one rational function into two or more rational
functions which are more easily integrated.
Think back to the steps taken when adding or subtracting fractions that do not
have the same denominator. First you find the lowest common multiple of the two
denominators and then cross multiply with the numerators accordingly. eg.
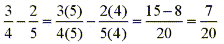
Well the same process applies when dealing with polynomial fractions. eg.
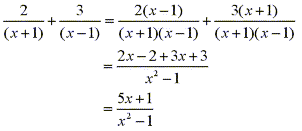
Now by reversing this process we can simplify a function such as
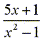 into two fractions into two fractions
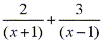 which are more easily integrated. which are more easily integrated.
This process is possible when the function is proper; that is the
degree of the numerator is less than the degree of the denominator. If the function is
improper; that is the degree of the numerator is greater than or equal to the degree of
the denominator, then we must first use long division to divide the denominator into the
numerator until we obtain a remainder, such that it's degree is less than the denominator.
Then if possible the above process is used to simplify the proper function.
To complete some of the problems in this section it will be useful to know the
table integral
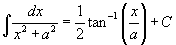
In general there are 4 cases to consider to express a rational function as the
sum of two or more partial fractions.
Case 1
The denominator is a product of distinct linear factors (no
factor is repeated or a constant mulptiple of another).
For example, 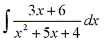
Since the degree of the numerator is less than the degree of the denominator we
don't need to divide. The denominator can be factored as follows:
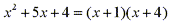
Since the denominator has distinct linear factors we can write the rational
fraction as the sum of two or more partial fractions as follows:
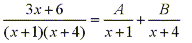
By multiplying both sides by 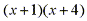 we have:
we have:
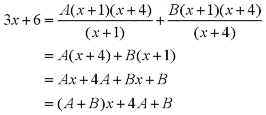
From this equation we can match terms of the same degree to determine
the coefficients by solving the following system of equations:
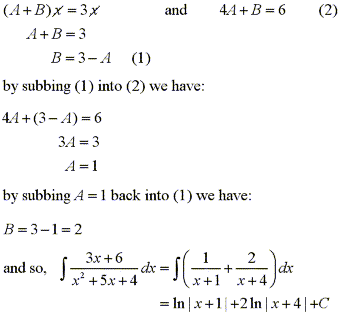
Case 2
The denominator is a product of linear functions, some of which are repeated.
For example, 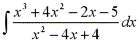
Since the degree of the numerator is greater than the degree of the denominator
we must factorize by long division.
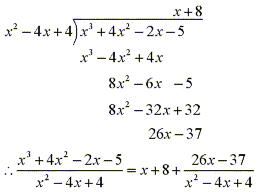
So we can now factor the denominator to obtain:
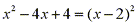
Since the linear factor (x-2) occurs twice, the partial fraction decomposition
is:
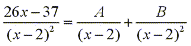
When we multiply both sides by the least common denominator we get:
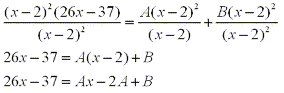
From this equation we can match terms of the same degree to determine
the coefficients by solving the following system of equations:
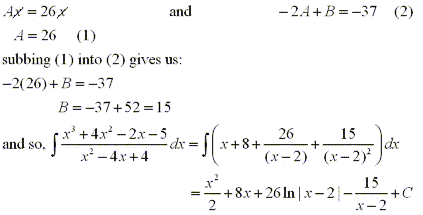
Case 3
The denominator contains irreducible quadratic factors, none of which are
repeated.
When reducing such functions to partial fractions if there is a term in the
denominator of the form ax2 + bx + c, where b2 - 4ac < 0, then the
numerator for that partial fraction will be of the form Ax + B.
For example, 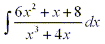
Since the degree of the numerator is less than the degree of the denominator
we do not have to divide first.
Since x3 + 4x = x(x2 + 4) can't be factored any further
we have:
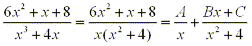
multiplying both sides by x(x2 + 4), we have:
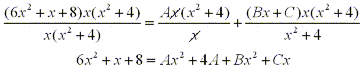
From this equation we can match terms of the same degree to determine the
coefficients by solving the following system of equations:

Case 4
The denominator contains a repeated irreducible quadtratic factor.
Functions of this form are the same as those in case 3 only there is a term
in the denominator that is repeated or is a constant multiple of another.
For example, 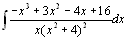
If we were to expand the denominator we would see that its degree is greater than
the the degree of the numerator so we do not have to divide first.
Since the function cannot be factored any further we have:
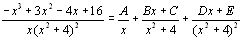
multiplying both sides by (x + 1)(x2 + 4)2, we have:
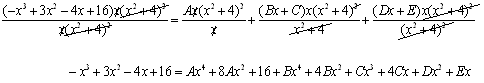
From this equation we can match terms of the same degree to determine the
coefficients by solving the following system of equations:
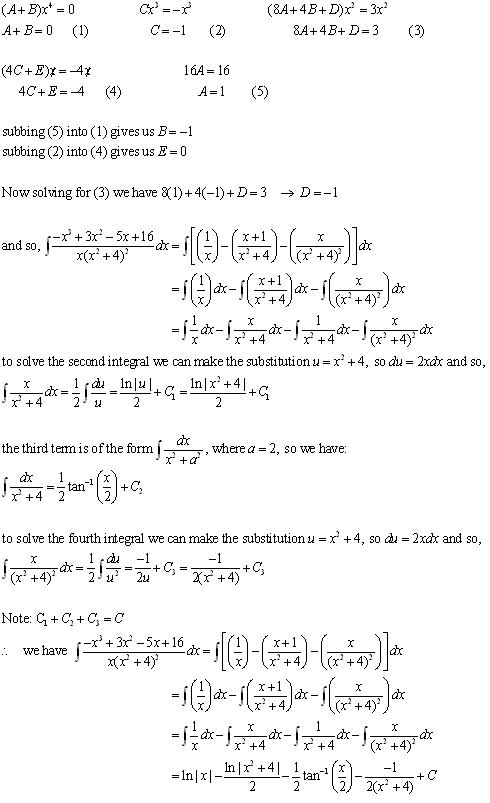
In all of the previous tutorials we have dealt with integrals with a continous
function f on a finite interval [a,b]. In this section we will consider two
types of integrals known as improper integrals. The first type of improper integral are
those defined on an infinite interval, and the second are those where the function f
has an infinite discontinuity in [a,b].
Type 1: Infinite Intervals
Type 2: Discontinous Integrands
For more practice with the concepts covered in
this tutorial, visit the Integral Problems page
at the link below.
The solutions to the problems will be posted after these chapters are
covered in your calculus course.
To test your knowledge of integration problems, try taking the
general integrals test on the iLrn website or the
advanced
integrals test at the link below.
Integral Problems
General Integrals Test on iLrn
Advanced Integrals Test
|Top
of Page |
|

