|
Before continuing with the curve sketching
tutorial, it's recommended that you review the maximum and minimum
values section of the related rates and optimization tutorial at the
link below.
Maximum
and Minimum Values
Curve sketching is another practical application
of differential calculus. We can make a fairly accurate sketch of any
function using the concepts covered in this tutorial.
The derivative of a function can tell us where
the function is increasing and where it is decreasing. If
a) f'(x) > 0 on an interval I, the function is
increasing on I.
b) f'(x) < 0 on an interval I, the function is decreasing on I.
The intervals of increase and decrease will occur
between points where f'(x) = 0 or f'(x) is undefined. However, these
points are not necessarily critical numbers because we include x even
if it is not in the domain of f. We simply want to find the intervals
of increase and decrease around x, even if the function is not defined
at that point.
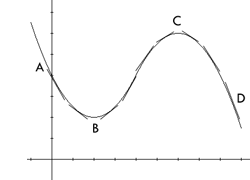
The graph to the right illustrates this theorem.
From A to B, the slope of the tangent lines are all negative, so the
derivative, f'(x) is negative from A to B. The theorem above states
that the function is decreasing from A to B. The graph shows that the
values of the function are decreasing between A and B. Similarly, the
function is also decreasing between C and D. From B to C however, the
slopes of the tangent lines are positive. Therefore, the derivative is
positive from B to C. The graph shows that the values of the function
are increasing between B and C.
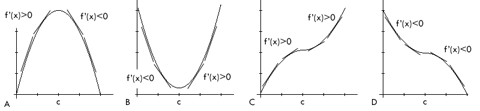
Let c be a critical number of a
continuous function f. If
a) f' changes from positive to negative at c,
there is a local maximum at c.
b) f' changes from negative to positive at c, there is a local
minimum at c.
c) f' does not change sign at c, (that is, the derivative is
positive before and after c or negative before and after c)
there is no maximum or minimum at c.
The graphs below illustrate the first derivative
test.
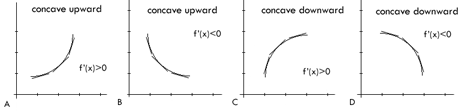
A graph is called concave upward (CU) on
an interval I, if the graph of the function lies above all of the
tangent lines on I. A graph is called concave downward (CD) on
an interval I, if the graph of the function lies below all of the
tangent lines on I.
The second derivative of a function can tell us
whether a function is concave upward or concave downward. If
a) f''(x) > 0 for all x in an interval I, the
graph is concave
upward on I.
b) f''(x) < 0 for all x in an interval I, the graph is concave
downward on I.
The intervals of concavity will occur between
points where f''(x) = 0 or f''(x) is undefined. We test the concavity
around these points even if they are not included in the domain of f.
The graphs below illustrate the different forms
of concavity. Remember that there are two ways in which a graph can be
concave upward or concave downward. Graphs A and C illustrate the types
of concavity when the function is increasing on the interval, while
graphs B and D illustrate concavity when the function is decreasing on
the interval. These 4 graphs cover every different form of concavity.
A point P on a curve is called a point of
inflection if the function is continuous at that point and either
a) the function changes from CU to CD at P
b) the function changes from CD to CU at P
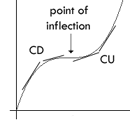
Points of inflection may occur at points where
f''(x) = 0 or f''(x) is undefined, where x is in the domain of f. We
must test the concavity around these points to determine whether they
are points of inflection.
The graph to the right illustrates a curve with a
point of inflection.
The Second Derivative Test
Let f be a continuous function near c. If
a) f'(c) = 0 and f''(c) > 0, then
f has a local minmum
at c.
b) f'(c) = 0 and f''(c) < 0, then f has a local
maximum at c.
The graphs containing local maximums and minimums
in the "Increasing and Decreasing Functions" and "The First Derivative
Test" sections above illustrate the second derivative test. When a
graph has a local minimum, the function is concave upward (and thus
lies above the tangent lines) at the minimum. Similarly, the function
is concave downward at a local maximum.
Examples
1
| Use the graph to find the following
2
| For the function f, find the following
Before continuing with asymptotes, it is
recommended that you review the vertical asymptote and infinite limits
section of the limits tutorial at the link below.
Vertical
Asymptotes and Infinite Limits
In order to properly sketch a curve, we need to
determine how the curve behaves as x approaches positive and
negative infinity. We must find the limit of the function as x
approaches infinity.
For a function f defined on (a, ¥),
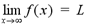
means that the values of f(x) approach the
value L when x is taken to be sufficiently large.
For a function f defined on (-¥,
a),
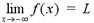
means that the values of f(x) approach the
value L when x is taken to be sufficiently large,
negatively.
The line y = L is called a horizontal
asymptote of y = f(x) if either,
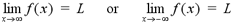
In order to find the horizontal asymptotes of a
function, we use the following theorem. If n is a positive
number, then
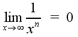
If n is a positive, rational number such
that xn is defined for all x, then
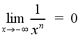
Functions do not always approach a value as x
approaches positive or negative infinity. Often there is no horizontal
asymptote and the functions have infinite limits at infinity. For
example, the function f(x) = x2 approaches
infinity when x is taken to be sufficiently large, positively or
negatively.
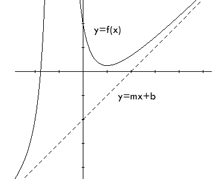
Slant Asymptotes
Some curves may have an asymptote that is neither
vertical nor horizontal. These curves approach a line as x
approaches positive or negative infinity. This line is called the slant
asymptote of the function. The graph to the right illustrates the
concept of slant asymptotes.
If
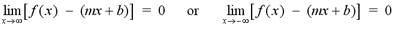
then the function f(x) has a slant
asymptote of y = mx + b.
Rational functions will have a slant asymptote
when the degree of the numerator is one more than the degree of the
denominator. To find the equation of the slant asymptote, we divide the
numberator by the denominator using long division. The quotient will be
the equation of the slant asymptote. The remainder is the quantity f(x)
- (mx + b). We must show that the remainder approaches 0, as x
approaches positive or negative infinity. The example below will give
you a better idea of how to find the slant asymptote of a function.
Examples
3
| Evaluate the limit
4
| Find the vertical and horizontal asymptotes of the function
5
| Find the equation of the slant asymptote of the function
The following steps are helpful when sketching
curves. These are general guidelines for all curves, so each step may
not always apply to all functions.
a) Domain: Find the domain of the function.
This will be useful when finding vertical asymptotes and determining
critical numbers.
b) Intercepts: Find the x- and y-intercepts
of the function, if possible. To find the x-intercept, we set y = 0 and
solve the equation for x. Similarly, we set x = 0 to
find the y-intercept.
c) Symmetry: Determine whether the
function is an odd
function,
an even function
or
neither
odd nor even. If f(-x) = f(x) for all x in the domain, then f is even
and symmetric about the y-axis. If f(-x) = -f(x) for all x in the
domain, then f is odd and symmetric about the origin.
d) Asymptotes: Find the asymptotes of the
function using the methods described above. First attempt to find the
vertical and horizontal asymptotes of the function. IF necessary, find
the slant asymptote.
e) Intervals of Increase and Decrease:
Using the methods described above, determine where f'(x) is positive
and negative to find the intervals where the function is increasing and
decreasing.
f) Local Maximum/Minimum : Find the
critical numbers of the function. Remember that the number c in the
domain is a critical number if f'(c) = 0 or f'(c) does not exist. Use
the first derivative test to find the local maximums and minimums of
the function.
g) Concavity and Points of Inflection : We
must determine when f''(x) is positive and negative to find the
intervals where the function is concave upward and concave downward.
Inflection points occur whenever the curve changes in concavity.
h) Sketch : Using the information
obtained from steps A to G, we can sketch the curve. First, we draw
dashed lines for the asymptotes of the function. Then plot the x- and
y-intercepts, maximum and minimum points and points of inflection on
the graph. Sketch the curve between the points, using the intervals of
increase and decrease and intervals of concavity. Be sure that the
graph behaves correctly when approaching asymptotes.
The examples below will give you a better idea of
how to follow these steps to sketch the graph of a function.
Examples
6 |
Sketch the graph of the function ( Steps A to D )
|
Sketch the graph of the function ( Steps E to H )
7 |
Sketch the graph of the function ( Steps A to D )
|
Sketch the graph of the function ( Steps E to H )
For more practice with the concepts covered in
this tutorial, visit the Curve Sketching Problems page
at the link below. The solutions to the problems will be posted after
these chapters are covered in your calculus course.
To test your knowledge of curve sketching problems, try taking the
general curve sketching test on the iLrn website or the advanced
curve sketching test at the link below.
Curve Sketching Problems
General Curve Sketching Test on iLrn
Advanced Curve Sketching Test
|Top
of Page |
|

