The logarithmic function is the inverse to the exponential function. A logarithm to the base b is the power to which b must be raised to produce a given number. For example, log₂8 is equal to the power to which 2 must be raised to in order to produce 8. Clearly, 2³ = 8 so log₂8 = 3. In general, for b > 0 and b not equal to 1,

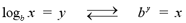
Some of the basic properties of logarithms are listed below. These properties are known as the cancellation equations, since they allow for the logarithmic expresion to be simplified to a single variable in specific situations.

NOTE: By convention, logarithms to the base 10 are simply referred to as log rather than log₁₀, since 10 is the most common base. For example, the log button on your calculator refers to logarithms to the base 10.

Examples

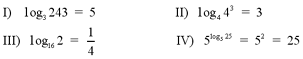
Laws of Logarithms

The following laws show how to calculate logarithms of a product, quotient or exponential expression. For any a, x, y > 0, where a does not equal and any real number r,

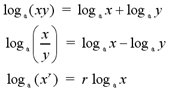
Two important facts that can be useful in logarithmic calculations are that log_b1 = 0 and log_bb = 1.

Examples

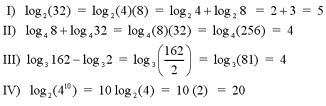
Note: For a complex example of expanding a logarithmic expression using the laws of logarithms, see question #1 in the Additional Examples section at the bottom of the page. For an example of solving a logarithmic expression, see question #2 in the Additional Examples section.

Natural Logarithms

A natural logarithm, denoted ln rather than log, is a logarithm with base e. The irrational number e is equal to 2.718281828459... This number has important applications in calculus and the true meaning of it will be explained in the Derivatives of Logarithmic Functions section. For now, it can be taken as a special number that is approximately equal to 2.718.

The notation for natural logarithms is a bit different than the notation for regular logarithms. The natural logarithm is equal to the logarithm with the base e.

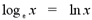
One special property of natural logarithms is that ln e = 1. This property is easily seen, since the logarithmic form of ln e is log_e e, which is always equal to 1 for any variable.

The definition of natural logarithms follows from the definition of regular logarithms, where

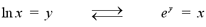
The cancellation equations for natural logarithms also follow from the property for regular logarithms.

The laws of logarithms can also be applied to natural logarithms by letting the base a equal e. The laws of natural logarithms are shown below. For any x,y > 0 and any real number r,

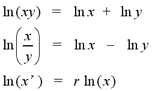
Examples

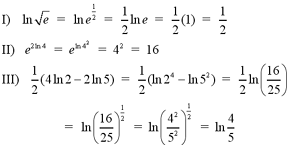
Note: For a complex example of solving a logarithmic expression, see question #3 in the Additional Examples section at the bottom of the page.

Change of Base Formula

As stated earlier, calculators are only able to calculate logarithms to the base 10 or e. The change of base formula allows us to calculate logarithms of any base with our calculators. The general change of base formula states

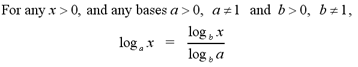
This formula can be modified to convert between logarithms and natural logarithms.

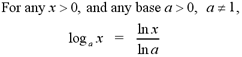
Examples

Additional Examples

| Top of Page |