|
|
COMMON MISTAKES
|
This section lists common mistakes that students
can sometimes make. For ease of reference the errors are divided into
four main categories. The Calculus
Errors
section deals with errors associated with derivatives and
integrals. The Root and Exponent
Errors
section deals with
errors involving exponents and roots. The Algebraic
Manipulation Errors section includes errors which may occur when
dealing with manipulating expressions. Finally, the Trigonometric Errors section deals
with common errors
involving trigonometry.
Note that these are listed by ERROR so the formula that appears above
the explanation is INCORRECT. The correct formula (if one exists)
appears
at the
end of the explanation.
- [f(x)g(x)]' = [f '(x)][g '(x)]
- Let us assume that this is true.
Let f(x)=x and g(x)=2x. Then we have:
[f(x)g(x)]' = [f '(x)][g '(x)]
[x(2x)]' = [(x)'][(2x)']
[2x2]' = 1(2)
4x = 2
This example clearly shows the error in assuming that [f(x)g(x)]' = [f
'(x)][g '(x)] since the incorrect answer (the right side) is not equal
to
the correct answer (the left side). The correct method to be used is
the Product
Rule
where [f(x)g(x)]' = [f '(x)][g(x)] + [f(x)][g '(x)].
- [f(x) / g(x)]' = [f '(x)] / [g '(x)]
- Let us assume that this is true.
Let f(x)=x and g(x)=2x. Then we have:
[f(x) / g(x)]' = [f '(x)] / [g '(x)]
[x / 2x]' = (x)' / (2x)'
[1 / 2]' = 1 / 2
0 = 1 / 2
From this example it can be seen that [f(x)g(x)]' = [f
'(x)][g '(x)] is the incorrect. The correct method to be used is the Quotient Rule
where [f(x) / g(x)]' = ( [f '(x)][g(x)] - [f(x)][g '(x)] ) / [g(x)]2.
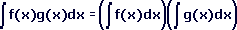
- Let us assume that this is true.
Let f(x)=x and g(x)=2x. Then we have:
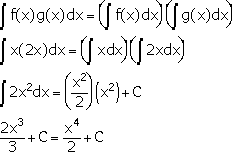
From this it is easy to see that evaluating the integral of a product
as the product
of two integrals gives the wrong answer. The correct method to
use here is the Substitution Rule (unless the
integral can be simplified and directly evaluated as with the above
example).
Note: The arbitrary constant
C is the same on both sides since
the assumption was that both sides of the equation were equal, hence
the constant is assumed to be the same on both sides.
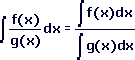
- Let us assume that this is true.
Let f(x)=x and g(x)=2x. Then we have:
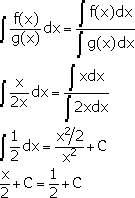
As can be seen the answer on the right is not equal to the answer on
the left (which is the correct answer) so this way of evaluating the
integral of a quotient is incorrect. The correct method to be
used is the Substitution
Rule (unless the integral can be simplified and directly evaluated
as with the above example).
Note: The arbitrary constant
C is the same on both sides since
the assumption was that both sides of the equation were equal, hence
the constant is assumed to be the same on both sides.
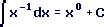
- If we were to use the Power Rule as this mistake
seems to suggest, we would actually have:
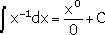
- Since division by 0 is undefined this method is
obviously incorrect. The correct answer to the integral is
ln|x|+C.
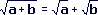
- Let us assume that this is true.
Let a=1 and b=4. Then we have:
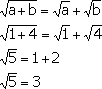
Since the square root of 5 is not equal to three we can see that you
cannot split the root in such a way.
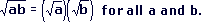
- Let us assume that the equation is
true.
Let a=-1 and b=-4. Then we have:
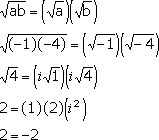
This example made use of complex
numbers. It can be shown that with
the use of complex numbers either a or b can be negative but not
both. However in MATH 1036/1037 we are only looking for real valued
answers so for this course, both a and b must be positive.
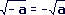
- Let us assume that the equation is
true.
Let a=-4. Then we have:
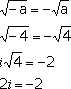
This example made use of complex
numbers. Since in MATH 1036/1037 only real valued answers are
desired
and (as shown in the example) the negative sign cannot be removed from
the square root, the correct response in this course would be "no
real valued answers exist".
- (cx)n = cxn where c is
constant.
- Let us assume that the equation is
true.
Let c=2, x=3, and n=2. Then we have:
(cx)n = cxn
((2)(3))2 = 2(32)
62 = 2(9)
36=18
It is quite clear that 36 is not equal to 18 so the assumption that
this is true is wrong. The correct formula for removing brackets
in this case is
(cx)n = cnxn.
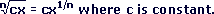
- Let us assume that the equation is
true.
Let c=8, x=8, and n=3. Then we have:
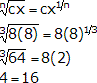
As 4 is not equal to 16 this formula is flawed. The correct
formula is 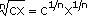 . .
- (x+y)2 = x2+y2
- Let us assume that the equation is
true.
Let x=2 and y=4. Then we have:
(x+y)2 = x2+y2
(2+4)2 = 22+42
62 = 4+16
36 = 20
Since 20 is not equal to 36 (36 being the correct answer) this formula
is wrong. The correct formula is (x+y)2 = x2+2xy+y2
because (x+y)2 means (x+y)(x+y).
- (-x)2 = -x2
- Let us assume that the equation is
true.
Let x=2. Then we have:
(-x)2 = -x2
(-2)2 = -22
4 = -(22)
4 = -4
This example shows that the negative sign cannot be factored from the
brackets when raised to the power 2. The correct way to solve this is
(-x)2 = x2. Note that this property holds
for any even power but if the exponent is odd the negative sign can be
factored as in the example.
-
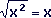
- Let us assume that the equation is
true.
Let x = -1. Then we have:
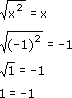
The correct way to simplify this is: 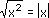
- x-(a-b) = x-a-b
- Let us assume that this is true. Let
x=2, a=3, and b=4. Then we have:
x-(a-b) = x-a-b
2-(3-4) = 2-3-4
2-(-1)= -5
2+1 = -5
3 = -5
As can be seen -5 is not equal to 3 so the formula is incorrect.
The error was that the negative sign must be multiplied into both terms
in the bracket leaving x-(a-b) = x-a+b.
- (ax2+b) / x = ax+b
- Let us assume that this is true. Let
x=2, a=3, and b=4. Then we have:
(ax2+b) / x = ax+b
(3(22)+4) / 2 = 3(2)+4
(3(4)+4) / 2 = 6+4
16 / 2 = 10
8 = 10
Since 10 does not equal 8 this formula is incorrect. The error
was believing that in dividing by x you only needed to remove x from
one term in the numerator. In order to do this EVERY term in the
numerator must have an x in it.
- ax2 = x solved by dividing both
sides by x. I.E. solve ax = 1
- Let us assume that this is true.
Let a=2. Then we have:
ax2 = x
ax = 1
2x = 1
x = 1/2
This seems plausible since we get a value for x and when substitute
into the equation it works. However, if we solve it the right way (by
subtracting x from both sides so the equation is equal to zero) we will
see why dividing by x is not the way to solve the equation.
ax2 = x
ax2-x = 0
x(ax-1) = 0
x(2x-1) = 0
so x = 0 or 2x-1 = 0
x = 0 or 2x-1 = 0
x = 0 or 2x = 1
x = 0 or x = 1/2
Therefore this method gives x = 1/2 as an answer as well but it also
gives x = 0 as another possible value for x. This means that the first
method is incorrect and the correct way to solve the equation is to
subtract x from both sides.
- 1 / (x+y) = 1/x + 1/y
- Let us assume that this is true. Let
x=2 and y=3. Then we have:
1 / (x+y) = 1/x + 1/y
1 / (2+3) = 1/2 + 1/3
1/5 = 3/6 + 2/6
1/5 = 5/6
Which is obviously false. It is often better to leave terms of this
type in their original form as splitting them up is usually more
difficult than evaluating directly.
- sin(x) = sin(x
 ) (note that the symbol beside the
second x is degree not power 0) ) (note that the symbol beside the
second x is degree not power 0)
- In calculus sin(x) means the sine of x
radians NOT x degrees. To show an example that these are
different, let x=2. Then we have:
sin(x ) = sin(2 ) = sin(2 ) )  0.03489950
0.03489950
sin(x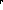 ) = sin(2 ) = sin(2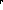 ) )  0.90929743
0.90929743
Even though the value of 2 was used in both equations, the difference
between 2 degrees and 2 radians made the answers different. Remember
that in calculus the value will almost always be in RADIANS.
This applies to all trigonometric terms, not just sin(x).
- sin(x+y) = sin(x) + sin(y)
- Let us assume that this is true. Let x=
 and y= and y= /6.
Then we have: /6.
Then we have:
sin(x+y) = sin(x) + sin(y)
sin( + + /6) =
sin( /6) =
sin( ) + sin( ) + sin( /6) /6)
sin(7 /6) = 0+1/2 /6) = 0+1/2
-1/2 = 1/2
This shows that the assumed formula is incorrect (since 1/2 is not
equal to -1/2). The correct formula in this situation is
- sin(x+y)
= sin(x)cos(y)+cos(x)sin(y). Formula for the other trigonometric
functions can be found in the Trigonometric Formulas
section.
Note that this applies to any trigonometric function and also for
'-' instead of '+'.
- cos-1(x) = 1 / cos(x)
- Let us assume that this is true. Let x=0.
Then we have:
cos-1(x) = 1 / cos(x)
cos-1(0) = 1 / cos(0)
 /2 = 1 / 1 /2 = 1 / 1
 /2 = 1 /2 = 1
Since  /2 is not equal to 1 so the
assumption is wrong. This is a common mistake since people often
think that because cos2(x)
= (cos(x))2 then cos-1(x) should equal (cos(x))-1.
However, cos-1(x) denotes the inverse cosine function, also
called arccosine, not the cosine function raised to the power -1. See
the Inverse
Trigonometric Functions section for more details. /2 is not equal to 1 so the
assumption is wrong. This is a common mistake since people often
think that because cos2(x)
= (cos(x))2 then cos-1(x) should equal (cos(x))-1.
However, cos-1(x) denotes the inverse cosine function, also
called arccosine, not the cosine function raised to the power -1. See
the Inverse
Trigonometric Functions section for more details.
Note that this observation applies for any trigonometric function.
|Top
of Page |
|
|
|
| QUESTIONS/COMMENTS |
|
Please forward any
questions,
comments, or problems you have experienced with this website to Alex Karassev.
|
|
|

