Perimeters, Areas, and Volumes
Perimeter is the distance around a two
dimensional (or flat) shape. Area (or surface area) is the
amount of space a two dimensional surface occupies. In a three
dimensional object, surface area is the area occupied by the
outer surface of the shape. Volume is the amount of space a
three dimensional object occupies. Here are formulas for the
perimeters, areas, and volumes of some basic shapes as well as sketches
of them.
Examples
Note: For another
example of finding the volume and surface area of a figure, see
question #1 in the Additional Examples section at the bottom of the
page.
Pythagoras Theorem
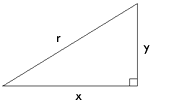
The Pythagorean Theorem is used to calculate side
lengths in right angled triangles. For hypotenuse r and sides x and y,
the Pythagorean theorem states :
r2 = x2 + y2
Given any two side lengths, this formula can be
used to calculate the third side.
Examples
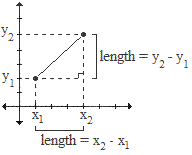
The formula for the distance between two points
(or length of a line segment) is derived from the Pythagorean Theorem.
This is shown in the figure to the right and the derivation below.
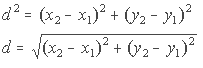
In summary, the distance D, between any two
points (x1, y1) and (x2, y2)
is given by:
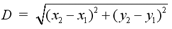
The midpoint of a line segment is the
point equidistant from both endpoints. If the endpoints of the line
segment are (x1, y1) and (x2, y2)
the midpoint is determined by the following formula:
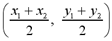
The x and y coordinates of the midpoint are the
averages of the x and y coordinates of the endpoints, respectively.
Examples
Note: For another
example of finding the midpoint and distance between two points, see
question #2 in the Additional Examples section at the bottom of the
page.
Circle Equation
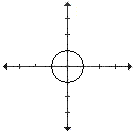
A unit circle has it's center at the origin (0,0)
and radius = 1. The general equation of the unit circle is x2
+ y2 = 1. To change this circle's position or size, we use
the following equation:
(x-h)2 + (y-k)2
= r2
where h is the factor by which the circle is
shifted right or left, k the factor by which the circle is shifted up
or down, and r the radius.
Note: In the formula,
(x-h) will shift the circle to the right and (x+h) will shift the
circle to the left. This is counter-intuitive from what would expect.
Common sense would tell us that (x+h) would mean a shift to the right
and (x-h) would shift to the left. This is not the case, however, so
watch for this error when working with circles. Similarly, (y-k) shifts
the circle upwards while (y+k) shifts the circle downwards. In
addition, remember that in the formula, the radius r is squared. So a
circle with equation x2 + y2 = 4 has a radius of
2 and not a radius of 4.
Examples
Other Conics
A conic is a shape which is made by intersecting
a plane with a cone. Aside from the circle, the other conic shapes are
the ellipse, hyperbola, and parabola. The table below lists the conics
and their corresponding formulas and sketches.
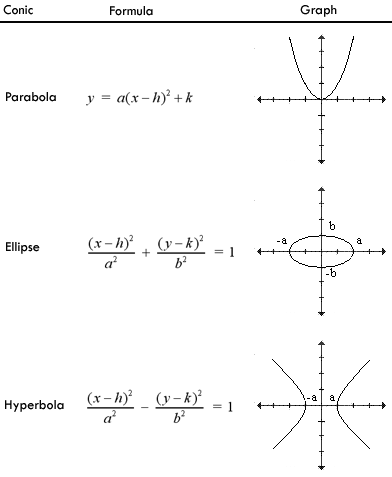
The manipulation of conics is similar to the
manipulation of circles, where h shifts the conic horizontally, k
shifts vertically and these two values, in the form (h,k), are the
coordinates of the center or vertex of the conic. The variables a and b
control the size and shape of the conic as r does with the circle.
Remember that a and b are squared, the same as r is squared in the
circle equation. See the note in the Circle Equation section for more
details.
The
quadratic equation tutorial has a more in depth look at the parabola.
Examples
Additional Examples
1
| Find the volume and surface area of the figure
2
| Find the midpoint and distance between points P and Q
|
Top of Page |
|

