Angles
The classical concept of trigonometry deals with
the relationships between the angles and sides of triangles. Over time,
however, trigonometry has
been adapted so that the angles do not necessarily represent angles in
a triangle. For example, in calculus, trigonometric functions are
defined for arbitrary real numbers.
Angles can be expressed in degrees
or radians. To convert a measurement from
radians to degrees (or vice versa) we use the following relationship:
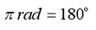
This relationship gives the following two
equations:
Note: By convention,
most angles are expressed in
radian measure, unless otherwise stated.
Examples
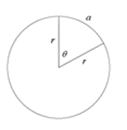
Arc Length
The arc length formula defines the relationship between arc length a,
radius r and the angle 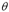 (in radians). (in radians).
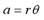
Note: Make sure that
your angles are measured in radians. The arc length formula does not
hold for angles measured in degrees. Use the conversion relationship
above to convert your angles from degrees to radians.
Note: For an example of
an arc length question, see question #1 in the Additional Examples
section at the bottom of the page.
Trigonometric Functions
The following ratios are for right angle
trigonometry. The angle must be acute (angle is less than
90°).
For angles that are obtuse (angle is
greater than 90°) or negative, we use the following trigonometric
ratios. The x and y variables are the values of the x and y
coordinates, respectively. The r variable represents the distance from
the origin, to the point (x,y). This value can be found using the
Pythagorean theorem.
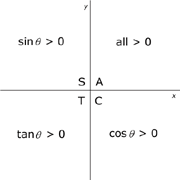 When
negative or obtuse angles are used in trigonometric
functions, they will sometimes produce negative values. The CAST graph
to the left will help you to remember the signs of trigonometric
functions for different angles. The functions will be negative in all
quadrants except those that indicate that the function is positive. For
example, When the angle is between 0° and 90° (0 and pi/2
radians), the line r is in the A quadrant. All functions will be
positive in this region. When the angle is between 90° and 180°
(pi/2 and pi radians), the line is in the S quadrant. This means that
only the sine function is positive. All other functions will be
negative. When
negative or obtuse angles are used in trigonometric
functions, they will sometimes produce negative values. The CAST graph
to the left will help you to remember the signs of trigonometric
functions for different angles. The functions will be negative in all
quadrants except those that indicate that the function is positive. For
example, When the angle is between 0° and 90° (0 and pi/2
radians), the line r is in the A quadrant. All functions will be
positive in this region. When the angle is between 90° and 180°
(pi/2 and pi radians), the line is in the S quadrant. This means that
only the sine function is positive. All other functions will be
negative.
Note: For examples of
finding trigonometric ratios see questions #2 and #3 in Additional
Examples at the
bottom of the page.
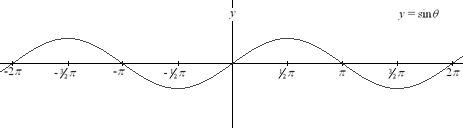
Sine Function
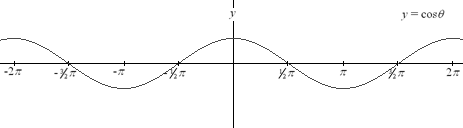
Cosine Function
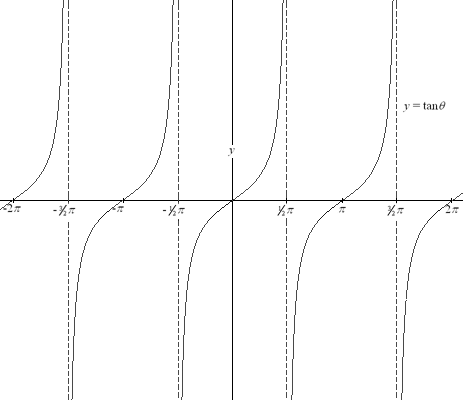
Tangent Function
Note: As illustrated in
the graphs above, the sine and cosine functions are defined for all
values of x. The tangent function, however, being equal to sin x / cos
x, is undefined whenever cos x = 0.
Periodicity of Trigonometric Function
From the graphs above, you can see that
trigonometric functions are periodic.
The sine and cosine functions,
for example, have a period of 2 pi. In general, for any integer k,
The tangent function, however, has a period of
pi. The period of the tangent function is given by
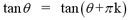
for any integer k.
This allows us to easily graph trigonometric
functions. We must only determine the graph of the function over its
period.
Examples of periodicity can be easily shown using
a calculator. For example, if you were to solve sin(160pi) using your
calculator, you would find that it is equal to sin(0)=0. This is
because sin(160pi) = sin(0 + 2pi(80)).
Using this concept of periodicity, we can
calculate certain trigonometric functions without using our
calculators. For example, tan(31pi/3) is equal to tan(pi/3 + pi(10)),
or equivalently tan(pi/3). From the table in the section below, we know
that tan(pi/3) is equal to the square root of 3. So, tan(31pi/3) is
also equal to root 3.
Special Triangles
|
I)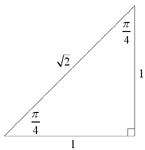
|
II)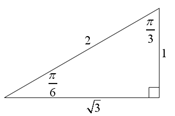
|
Using the "special" triangles above, we can find
the exact trigonometric ratios for angles of pi/3, pi/4 and pi/6. These
triangles can be constructed quite easily and provide a simple way of
remembering the trigonometric ratios. The table below lists some of the
more common angles (in both radians and degrees) and their exact
trigonometric ratios.

The Laws of Sines and Cosines
The laws of sines and cosines are useful in
determining the sides and angles of oblique triangles. All
triangles that are not right angled are classified as oblique
triangles. The oblique triangle below will be used in the definitions
for the laws of sines and cosines.
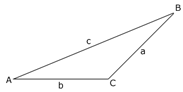
The law of sines states:
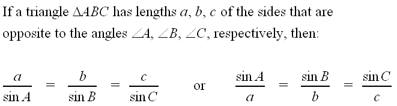
Note: All the sides and
angles of a triangle can be determined using the law of sines if you
know the measurements of any 2 angles and any one side.
Note: For an example of
solving a triangle using the sine law, see question #4 in the
Additional Examples section at the
bottom of the page.
The law of cosines states:
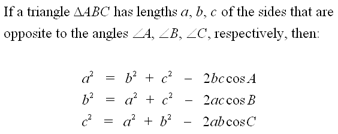
Note: All sides and
angles of a triangle can be determined using the law of cosines if you
know the measurements of 2 sides and the angle enclosed between them,
or the lengths of all 3 sides.
Note: For an example of
solving a triangle using the cosine law, see question #5 in the
Additional Examples section at the
bottom of the page.
•
| Proof of the cosine law
Trigonometric Identities
The identities listed below are the basic
trigonometric identities. They can be combined with one another to
create many more identities.
The trigonometric formulas below can be combined
with the identities above to create very complex trigonometric
identities. These formulas are often necessary when proving
trigonometric identities.
Note: For an example of
proving a trigonometric identity, see question #6 in the Additional
Examples section below.
Additional Examples
1
| Find the angle, given arc length and radius
2
| Find all trigonometric ratios of the triangle
3 |
Find
the exact trigonometric ratios for a given angle
4
| Solve the triangle using the law of sines
5
| Solve the triangle using the law of cosines
6
| Prove the trigonometric identity
|
Top of Page |
|

