Series Notation
A sequence is an ordered set of numbers
that most often follows some rule (or pattern) to determine the next
term in the order. For
example, x, x2, x3, x4, ... is a
sequence of numbers, where each successive term is multiplied by x.
A series is a summation of the terms of a
sequence. The greek letter sigma 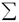 is used to represent the summation
of terms of a sequence of numbers. Series are typically written in the
following form:
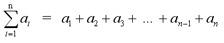
where the index of summation, i
takes consecutive integer values from the lower limit, 1 to the
upper limit, n. The term ai is
known as the general term.
A finite series is a summation of a
finite number of terms. An infinite series has an infinite
number of terms and an upper limit of infinity. This tutorial will deal
with finite series. Infinite series will be covered in the calculus
tutorials.
Examples
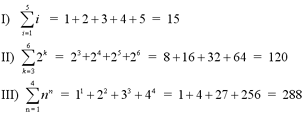
Types of Sequences/Series
There are two main types of sequences. An arithmetic
sequence is one in which successive terms differ by the same
amount. For example, {3, 6, 9, 12, ...} is an example of an arithmetic
sequence, where each term is obtained by adding 3 to the previous term.
A geometric sequence is one in which the quotient of any two
successive terms is a constant. For example, {3, 9, 27, 81, ...} is an
example of a geometric sequence, where each term is obtained by
multiplying the previous term by 3. Similarly, there are also arithmetic
series and geometric series, which are simply summations of
arithmetic and geometric sequences, respectively.
General theorems for arithmetic series and
geometric series are listed in the Theorems of Finite Series section
below
Properties of Finite Series
The following are the properties for
addition/subtraction and scalar multiplication of series. These
properties will help to calculate series whose general term is a
polynomial.
Theorems of Finite Series
The following theorems give formulas to calculate
series with common general terms. These formulas, along with the
properties listed above, make it possible to solve any series with a
polynomial general term, as long as each individual term has a degree
of 3 or less.
•
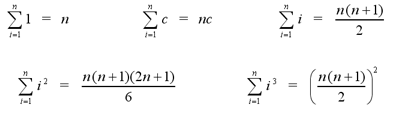
| Proof of finite series theorem with general term i
The following theorem is used for calculating
arithmetic series. Suppose we have the following arithmetic series, {a
+ (a+d) + (a+2d) + ... + (a+(n-1)d}. Then,
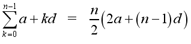
The following theorem is used for calculating
geometric series. Suppose we have the following geometric series, {a +
ar + ar2 + ... + ar(n-1)}. Then,
•
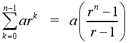
| Proof of geometric series theorem
Examples
Note: For another
example of finding the sum of a series, see question #1 in the
Additional Examples section at the
bottom of the page.
Telescoping Sums
A telescoping sum is a summation where
successive terms cancel each other out. For example,
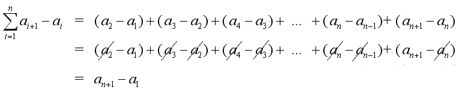
is a telescoping sum. This type of series can be
easily calculated since all but a few terms are cancelled out.
Note: For an example of
a telescoping sums question, see question #2 in the Additional Examples
section below.
Additional Examples
1
|
Determine the sum of the series
2
| Evaluate the telescoping sum
3
|
Determine the sum of the geometric series
|
Top of Page |
|
