|
The average rate of change of a function y=f(x)
from x to a is given by the equation
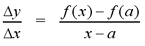
The average rate of change is equal to the slope
of the secant line that passes through the points (f, f(x)) and (a,
f(x)). As x approaches a along the curve, the secant line approaches
the tangent line to the curve at a. The slope of the tangent line at a
is equal to the instantaneous rate of change of the function at a. This
slope can be calculated by taking the limit of the average rate of
change, as x approaches a.
A derivative is the instantaneous rate of
change of a function. When finding the equation of tangent lines, the
slope of the curve f(x) at (a, f(a)) is equal to
the derivative of f at a. When finding
rates of change, the instantaneous rate of change of a function f(x)
when x=a is equal to the derivative of f at a.
Derivatives have their own notation. The
derivative of a function f at a number a is denoted by f'(a)
and is given by:
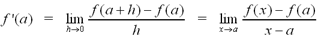
So f'(a) represents the slope of the tangent line
to the curve at a, or equivalently, the instantaneous rate of change of
the function at a.
Note: If we let x=a+h,
then as h approaches 0, x will approach a+(0), or simply a. By
rearranging x=a+h, we have h=x-a. If we substitute these relations into
the limits above, we will find that the two definitions of derivative
are equivalent.
Examples
1
| Find the derivative of the function f
2
| Find the equation of the tangent line to the curve y=f(x) at point P
In addition to the notation above, there are
several other notations for expressing the derivative of a function.
The most common notations are :
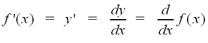
The notation 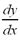 is called Leibniz
notation. It is the most commonly used notation after the f'(x)
notation. is called Leibniz
notation. It is the most commonly used notation after the f'(x)
notation.
If we find the derivative for the variable x
rather than a value a, we obtain a derivative function with
respect to x. With this function, the derivative at any value
of x can be determined. By replacing a with x
in the limit formula, we can find the derivative function.
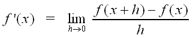
Examples
3
| Find the derivative of the function f at points A, B, C
A function is differentiable at a
if f'(a) exists. It is differentiable on the open interval (a,
b) if it is differentiable at every number in
the interval.
If a function is differentiable at a then
it is also continuous at a. The contrapositive of this theorem
states
that if
a function is discontinuous at a then it is not differentiable
at a.
A function is not differentiable at a if
its graph illustrates one of the following cases at a :
Discontinuity
A function is not differentiable at a if
there is any type of discontinuity at a. This is stated in the
contrapositive of the theorem above. The graph to the right illustrates
jump discontinuity.
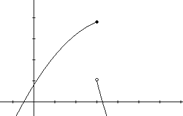
Vertical Tangent Line
A function is not differentiable at a if
its graph has a vertical tangent line at a. The tangent line to
the curve becomes steeper as x approaches a until it
becomes a vertical line. Since the slope of a vertical line is
undefined, the function is not differentiable in this case.
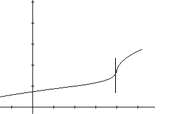
Corner
A function is not differentiable at a if
its graph has a corner or kink at a. As x approaches the corner
from the left- and right-hand sides, the function approaches two
distinct tangent lines. Since the function does not approach the same
tangent line at the corner from the left- and right-hand sides, the
function is not differentiable at that point. The graph to the right
illustrates a corner in a graph.
Note: Although a
function is not differentiable at a corner, it is still continuous at
that point.
Examples
4
| Find all points where the function is not differentiable
5
| Show that the function is not differentiable at x=a
Taking limits to find the derivative of a
function can be very tedious and complicated. The formulas listed below
will make differentiating much easier. Each formula is expressed in the
regular notation as well as Leibniz notation.
Constant Rule: If f is a constant
function, where f(x) = c, then

Power Rule: If f is a power function,
where f(x) = xn and n is a real
number, then
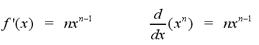
Note: The graph of the
derivative of a power function will be one degree lower than the graph
of the original function.
Note: For an example of
a power function question, see Example #6 below.
Constant Multiple Rule: If f is a
differentiable function and c is a constant, then
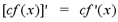
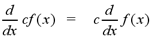
Sum Rule: If f and g are differentiable
functions, then
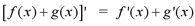
In Leibniz notation,
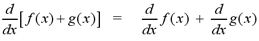
Note: For an example of
the sum rule, see Example #7 below.
Difference Rule: If f and g are
differentiable functions, then
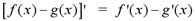
In Leibniz notation,
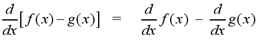
Note: For an example of
the difference rule, see Example #8 below.
Product Rule: If f
and g are
differentiable functions, then
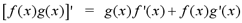
In Leibniz notation,
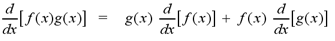
Note: For an example of
the product rule, see Example #9 below.
Quotient Rule: If f
and g are
differentiable functions, then
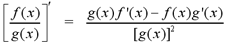
In Leibniz notation,
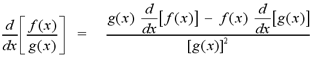
Note: For an example of
the quotient rule, see Example #10 below.
Examples
6
| Find the derivative using the power rule
7
| Find the derivative using the sum rule
8
| Find the derivative using the difference rule
9
| Find the derivative using the product rule
10
| Find the derivative using the quotient rule
The chain rule is used to find the
derivatives of compositions of functions. A composite function
is a function that is composed of two other functions. For the two
functions f and g, the composite function or the composition of f and
g, is defined by
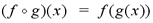
The function g(x) is substituted for x
into the function f(x). For example, the function F(x)=(2x+6)4
could be considered as a composition of the functions, f(x)=x4
and g(x)=2x+6. However, it could also be written as a
composition of f(x)=(2x)4 and g(x)=x+3.
Often, a function can be written as a composition of several different
combinations of functions.
The chain rule allows us to find the derivative
of composite functions. The chain rule states that if f and g are
differentiable functions and F(x)=f(g(x)), then F is
differentiable and the derivative of F is given by
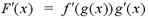
In Leibniz notation, if y=f(u), u=g(x)
and y and u are differentiable functions, then
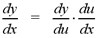
Examples
11
| Find the derivative using the chain rule
The limits below are required for proving the
derivatives of trigonometric functions. These limits and the
derivatives of the trigonometric functions will be proven in your
calculus lectures. Here, they are simply stated.
Note: These limits are
used often when solving trigonometric limit problems. Try to remember
them and the conditions under which they hold.
The derivatives of the six trigonometric
functions are shown below.
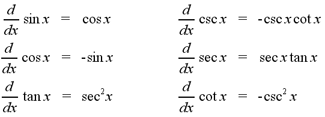
Note: The derivatives
of the co-functions (cosine, cosecant and cotangent) have a "-" sign at
the beginning. The derivatives of the other 3 functions have a "+" sign
at the beginning.
This is a helpful way to remember the signs when taking the derivatives
of trigonometric functions.
Examples
12
| Find the derivative of the trigonometric function
13
| Evaluate the limit
The method of implicit differentiation
allows us to find the derivative of an implicit function. It allows us
to
differentiate y without solving the equation explicitly. We can
simply differentiate both sides of the equation and then solve for y'.
When differentiating a term with y, remember that y is
a function of x. The term is a composition of functions, so we
use the chain rule to differentiate. For example, if you were to
differentiate the term 3y4 it would become (12y3)(y').
Note: For a more
concrete demonstration of how to differentiate implicit functions, see
example #14 below.
Examples
14
| Find the derivative by implicit differentiation
Earlier in the derivatives tutorial, we saw that
the derivative of a differentiable function is a function itself. If
the derivative f' is differentiable, we can take the derivative of it
as well. The new function, f'' is called the second derivative
of f. If we continue to take the derivative of a function, we can find
several higher derivatives. In general, f (n) is called the
nth derivative of f.
Note: Recall that when
working with motion application problems, the velocity of the particle
is the first derivative of the displacement function. The acceleration
of the particle is the derivative of the velocity function, or
equivalently, the second derivative of the displacement function.
Examples
15
| Find the higher derivatives of y
16
| Find the first and second derivatives of the function
It is often easy to calculate the exact value of
a function at a point a, but rather difficult to compute values
near a. For example, Ö9 is
quite easy to calulate while Ö8.94 is
rather difficult to calculate.
We can find an approximate value of the function
at points near a by using the tangent line to the curve at a.
If the function y=f(x) is differentiable at a,
then the linear approximation (or linearization) of f
at a is given by :
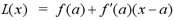
Examples
17
| Find the linear approximation of f at a
For more practice with the concepts covered in
the derivatives tutorial, visit the Derivatives Problems page at the
link below.
The solutions to the problems will be posted after the derivatives
chapter is covered in your calculus course.
To test your knowledge of derivatives, try taking the general
derivative test on the iLrn website or the advanced derivative test at
the link below.
Derivative
Problems
General Derivative Test on iLrn
Advanced
Derivative Test
|
Top of Page |
|

