Real Numbers
The set of real numbers is represented by the
letter R. Every number (except complex numbers) is contained in the set
of real numbers. When the general term "number" is used, it refers to a
real number. All of the following types or numbers can also be thought
of as real numbers.
Integers
The set of integers is represented by the letter
Z. An integer is any number in the infinite set,
Z = (..., -3, -2, -1, 0, 1, 2, 3,
...}
Integers are sometimes split into 3 subsets, Z+,
Z- and 0. Z+ is the set of all positive integers
(1, 2, 3, ...), while Z- is the set of all negative integers
(..., -3, -2, -1). Zero is not included in either of these sets . Znonneg
is the set of all positive integers including 0, while Znonpos
is the set of all negative integers including 0.
Natural Numbers
The set of natural numbers is represented by the
letter N. This set is equivalent to the previously defined set, Z+.
So a natural number is a positive integer.
N = { 1, 2, 3, 4, ... }
Whole Numbers
The set of whole numbers is represented by the
letter W. This set is equvalent to the previously defined set, Znonneg.
So a whole number is a member of the set of positive integers (or
natural numbers) or zero.
W = { 0, 1, 2, 3, 4, ... }
Rational Numbers
The set of rational numbers is represented by the
letter Q. A rational number is any number that can be written as a
ratio of two integers. The set of rational numbers contains the set of
integers since any integer can be written as a fraction with a
denominator of 1. A rational number can have several different
fractional representations. For example, 1/2 is equivalent to 2/4 or
132/264. In decimal representation, rational numbers take
the form of repeating decimals. Some examples of rational numbers are:
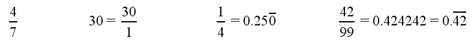
Irrational Numbers
The set of irrational numbers is represented by
the letter I. Any real number that is not rational is irrational. These
are numbers that can be written as decimals, but not as fractions. They
are non-repeating, non-terminating decimals. Some examples of
irrational numbers are:
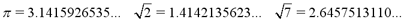
Note: Any root that
is not a perfect root is an irrational number. So any roots such as the
following examples, are irrational.
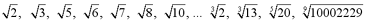
•
| Proof that the square root of 2 is irrational
|
Top of Page |
|

