Set Notation
A set is a collection of objects. Each
object in the set is called an element of the set. If an
element x is a member of the set S, we write  . If an element x is not
a member of the set S, we write . If an element x is not
a member of the set S, we write 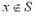 . The empty set is
the set that contains no elements. It is represented by {} or . The empty set is
the set that contains no elements. It is represented by {} or  . For sets A and B,
A is called a subset of B,
denoted . For sets A and B,
A is called a subset of B,
denoted 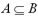 , if every element
of A is also an element of B. , if every element
of A is also an element of B.
The union of two sets A and B,
denoted 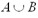 is the set that
consists of all elements that are in A or in B (or in
both A and B). The intersection of two sets A
and B, denoted is the set that
consists of all elements that are in A or in B (or in
both A and B). The intersection of two sets A
and B, denoted 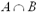 is the set that consists of all elements that are in A and in B.
is the set that consists of all elements that are in A and in B.
Sets are commonly defined in roster notation
or set-builder notation. Roster notation provides a listing of
each element in the set. For example, the set P of prime
numbers between 0 and 10 (excluding 0 and 10) in roster notation is
written as:
P = { 2, 3, 5, 7 }
The set-builder notation defines a general
element of the set and then provides a ruling for each element in the
set. The previous example, in set-builder notation is written as:
P = {x | x
is prime and 0 < x < 10}
Examples
Note: For another
example of intersections and unions of sets, see question #1 in the
Additional Examples section at the bottom of the page.
The Real Number Line
Every real number can be associated with a single
point on the real number line
Intervals
An interval is a set that consists of all
real numbers between a given pair of numbers. It can also be thought of
as a segment of the real number line. An endpoint of an
interval is either of the two points that mark the end of the line
segment. An interval can include either endpoint, both endpoints or
neither endpoint. To distinguish between these different intervals, we
use interval notation.
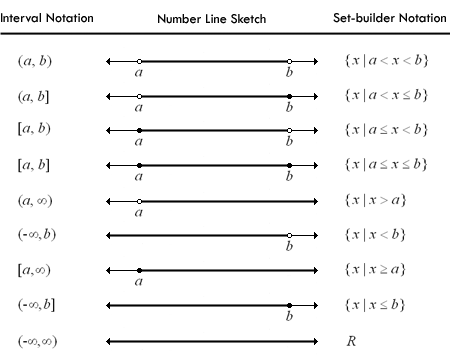
An open interval does not include
endpoints. The exclusion of the endpoints is indicated by round
brackets () in interval notation. When the interval is represented by a
segment of the real number line, the exclusion of an endpoint is
illustrated by an open dot. For example, the interval of numbers
between the integers 3 and 8, excluding 3 and 8, is written as
(3, 8) = {x | 3 < x
< 8 }
in interval notation. As a segment of the real
number line, it would be represented by the line below.

A closed interval includes the endpoints.
The inclusion of the endpoints is indicated by square brackets [] in
interval notation. When the interval is represented by a segment of the
real number line, the inclusion of an endpoint is illustrated by a
closed dot. For example, the interval of numbers between the integers 1
and 11, including both 1 and 11, is written as
[1, 11] = {x | 1 £ x £
11 }
in interval notation. As a segment of the real
number line, it would be represented by the line below.

One endpoint of an interval can be included,
while the other is excluded. The interval [a, b)
represents all numbers between a and b, including a
but not b. Similarly, the interval (a, b] would
represent all of the numbers between a and b, including
b but not a. These intervals are shown
in more detail in the table below.
Infinite intervals are those that do not
have an endpoint in either the positive or negative direction, or both.
The interval extends forever in that direction. Infinite intervals are
summarized in the table below.
Note: For an example
involving intervals, see question #1 in the Additional Examples section
below
Additional Examples
1
| Example of the intersection and union of intervals
|
Top of Page |
|

