|
A fraction is a ratio of two values.
Fractions have the form 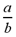 , where a is called the numerator, b is called
the denominator and b cannot equal 0 (since division by 0 is
undefined). , where a is called the numerator, b is called
the denominator and b cannot equal 0 (since division by 0 is
undefined).
Reducing Fractions
Fractions can be reduced if the numerator and
denominator have a greatest common divisor(gcd) greater than 1. The gcd
refers to the largest possible integer that will divide evenly into
each value. For example, gcd(6,18) = 6, since 6/6 = 1 and 18/6 =3. Six
is the largest integer that will divide evenly into each number. If
this example were a fraction, we would have
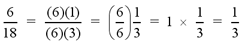
Greatest
Common
Divisor / Least Common Multiple Calculator
Examples
Converting Decimals to Fractions
Any rational number has a fractional
representation. Decimals can be written as fractions if they are
terminating or repeating. The following examples will show the step by
step method of how to convert a decimal to a fraction.
Examples
Note: For a more
complex example of decimal to fraction conversion, see question #1 in
the Additional Examples section at the bottom of the page.
Addition and Subtraction of Fractions
When adding or subtracting fractions, they must
have the same denominator. If they do not have the same denomimator, we
must find a common one for both. To do this, we first need to find the
lowest common multiple of the two denominators. The lowest common
multiple is the smallest number that both denominators will divide into
evenly. For example, the lowest common multiple of 2 and 3 is 6.
Next, we must multiply each fraction by the
proper integers so that they will have the same denominator. Continuing
our example, if the two fractions are 1/2 and 1/3, we get:

Now that the two fractions have the same
denominator, we can simply add or subtract them.

Examples
Improper Fractions and Mixed Numbers
Fractions can be written as improper fractions or
mixed numbers.
Improper fractions (ex. 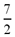 ) are
fractions that have a numerator larger than their denominator. ) are
fractions that have a numerator larger than their denominator.
Mixed numbers (ex. 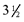 ) have an
integer value followed by a proper fraction. ) have an
integer value followed by a proper fraction.
To convert from an improper fraction to a mixed
number, we first divide the numerator by the denominator. The whole
number becomes the integer in the mixed number. Any remainder from the
divison is placed over the denominator and becomes the proper fraction.
To convert from a mixed number to an improper
fraction, we first convert the integer to a fraction by multiply the
integer value by the denominator in the proper fraction and placing it
over the denominator. Add the resulting fraction to the proper fraction
portion of the mixed number.
Examples
Multiplication and Division of Fractions
When multiplying two fractions, simply multiply
the two numerators and multiply the two denominators. For example,
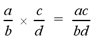
When dividing two fractions, the first fraction must be multiplied by
the reciprocal of the second fraction. For example,
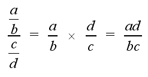
Examples
Additional Examples
1
| Example of decimal to fraction conversion
|
Top of Page |
|

