|
A linear equation is an equation whose
graph is a straight line. A linear equation in one variable is
an equation that simlpy involves x. There are no terms involving x2,
x3, x1/2 etc. Each term has a degree of at most
1. All operations, such as addition or multiplication, involve only x
and numerical constants. 3x + 4 = 5 is an example of a linear equation.
2(x+1) = 6(x-4) is also a linear equation. These equations can be
solved very easily by performing algebraic operations to the equation
to isolate x.
A linear equation in two variables is,
as the name suggests, an equation that involves 2 variables. The
standard form of this type of equation is Ax + By = C, where A,B and C
are real numbers. For example, 3x + y = 7 is a linear equation in two
variables. y = 2x + 1/3 is also an example, since it can be rewritten
as 2x - y = -1/3 ( or equivalently 6x - 3y = -1 ).
Slope-Intercept Form
Linear equations in two variables can also be
expressed in the slope-intercept form y = mx + b.
The slope of a line, represented by the variable m, is defined
as the ratio of change in values of y to change in value of x. The
slope is also known as rise over run. For any two points (x1
,y1), (x2 ,y2) on a line L, the
formula for calculating the slope of L is:
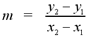
The y-intercept, denoted b, is the point
(0,b), where the line intercepts the y-axis.
There are two variations of the slope-intercept
form of a line. The first is called the point-slope form of the
equation of a line. This formula is used when the slope and a single
point on the line are given in the problem. The formula for the
point-slope form is:
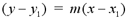
The other variation is the two-point form
of the equation of a line. This is simply the point-slope formula, with
the slope formula substituted for m. This formula should be used when
two points on a line are given in the problem. the formula for the
two-point form is:
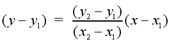
The vertical line x = a represents a special case
of the slope-intercept form of a line. Since (x2 - x1)
= 0, the slope of the line is m = (y2 - y1)/0.
Since division by 0 is undefined, the slope of the line is undefined.
The line is also expressed
in terms of x, rather than y. Due to these properties, vertical lines
cannot be expressed using the slope-intercept form.
Examples
Note: For another
example of finding the equation of a line, see question #1 in the
Additional Examples section at the
bottom of the page.
Line Theorems
Two lines are parallel if they have equal slopes.
Parallel lines never cross each other. The distance between two
parallel lines is always the same for every point along the lines.
Two lines are perpendicular, meaning their angle
of intersection is 90°, if their slopes are negative reciprocals of
each other. For lines L1 and L2 with slopes m1
and m2, respectively,
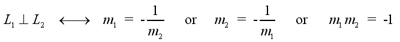
The midpoint of a line segment joining any two
points (x1,
y1) and (x2, y2) is the point given by:
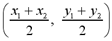
The distance, D, between any two points (x1,
y1) and (x2, y2) is given by:
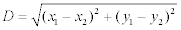
For
more information about distance and midpoint problems, visit the
Geometry Tutorial.
Graphing Linear Equations
Linear equations in one variable have graphs of
either horizontal or vertical lines, depending on which co-ordinate
plane variable is used. For equations of the form x = a, the graph is a
vertical line, intersecting the x-axis at (a,0). For equations of the
form y = b, the graph is a horizontal line intersecting the y-axis at
(0,b).
Linear equations are simply straight lines. If
you can determine two points that lie on a line, then the graph is the
line that connects those two points. This is sometimes referred to as
the two point method of graphing linear equations.
The most common points to determine from the
equation are the x and y intercepts, (x,0) and (0,y), respectively.
These points can be determined by substituting x = 0 and y = 0 into the
equation and finding the corresponding y and x values.
The slope-intercept method can also be
used to graph linear equations. The equation should be written in
slope-intercept form so the slope and y-intercept can be easily
identified. After plotting the y-intercept on the graph, a second point
can be obtained using the ratio of the slope. The graph is simply the
line that connects these points.
Examples
Note: For another
example of graphing a linear equation, see question #1 in the
Additional Examples section below.
Additional Examples
1
| Find and graph the equation of the line
|
Top of Page |
|

