|
Exponential expressions have the form xa,
where x is the base and a is the exponent. xa refers to the
product,
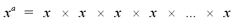
where there are 'a' factors of the term x. For
example,
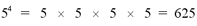
The exponential expression x0 is equal
to 1 for all x that are not equal to 0. When 0 is raised to an exponent
of 0 (00),
the expression is undefined.
Exponents can take on different values, such as
negative integers and fractions. The following formulas show how to
calculate these types of exponential expressions.
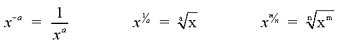
Note: In general, 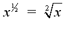 is simply written as is simply written as 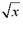 . In the expression x1/a,
if a is even, then x cannot be negative or it will be undefined. . In the expression x1/a,
if a is even, then x cannot be negative or it will be undefined.
Examples
Laws of Exponents
The following laws must be followed when
multiplying and dividing powers. Laws a) and b) only apply when the two
powers have the same base. Laws c) and d) only apply when the two
bases are raised to the same exponent.
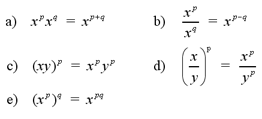
Examples
Note: For a complex
example of simplifying an exponential expression, see question #1 in
the Additional Examples section
below.
Additional Examples
1 |
Simplify the exponential expression
|
Top of Page |
|

