|
A quadratic equation is a trinomial of
the form ax2 + bx + c = 0. There are three main ways of
solving quadratic equations, that are covered below.
Factoring
Review
the factoring sections of polynomials tutorial
If a quadratic equation can be factored, then it
can be written as a product of two binomials. Since the trinomial is
equal to 0, one of the two binomial factors must also be equal to zero.
By factoring the quadratic equation, we can equate each binomial
expression to zero and solve each for x.
Examples
Completing the Square
Quadratic equations cannot always be solved by
factoring. They can always be solved by the method of completing
the squares. To complete the square means to convert a quadratic to
its standard form. We want to convert ax2+bx+c = 0 to a
statement of the form a(x - h)2 + k = 0. To do this, we
would perform the following steps:
1) Group together the ax2 and bx terms
in parentheses and factor out the coefficient a.
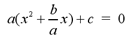
2) In the parentheses, add and subtract (b/2a)2,
which is half of the x coefficient, squared.
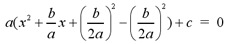
3) Remove the term - (b/2a)2 from the
parantheses. Don't forget to multiply the term by a, when removing from
parentheses.
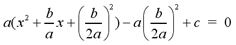
4) Factor the trinomial in parentheses to its
perfect square form, (x + b/2a)2.
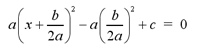
Note: If you group the
- (b/2a)2 + c terms together in parentheses, the equation
will now be in standard form. The equation is now much simpler to graph
as you will see in the Graphing section below. To solve the quadratic
equation, continue the following steps.
5) Transpose (or shift) all other terms to the
other side of the equation and divide each side by the constant a.
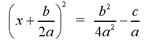
6) Take the square root of each side of the
equation.
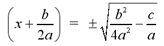
7) Transpose the term -b/2a to the other side of
the equation, isolating x.
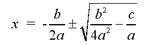
The quadratic equation is now solved for x. The
method of completing the square seems complicated since we are using
variables a,b and c. The examples below show use numerical coefficients
and show how easy it can be.
Examples
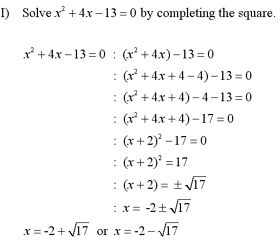
Note: For more examples
of solving a quadratic equation by completing the square, see questions
#1 and #2 in the Additional Examples section at the bottom of the page.
The Quadratic Formula
The method of completing the square can often
involve some very complicated calculations involving fractions. To make
calculations simpler, a general formula for solving quadratic
equations,
known as the quadratic formula, was derived. To solve quadratic
equations of the form ax2 + bx + c = 0, substitute the
coefficients a,b and c into the quadratic formula.
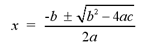
Derivation
of the Quadratic Formula
The value contained in the square root of the
quadratic formula is called the discriminant. If,

Examples
Graphing Quadratic Equations
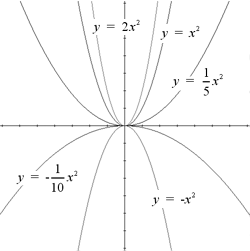
The graphical representation of quadratic
equations are based on the graph of a parabola. A parabola is an
equation of the form y = a x2 + bx + c. The most general
parabola, shown at the right, has the equation y = x2.
The coefficent, a, before the x2 term
determines the direction and the size of the parabola. For values of a
> 0, the parabola opens upward while for values of a < 0, the
parabola opens downwards. The graph at the right also shows the
relationship between the value of a and the graph of the parabola.
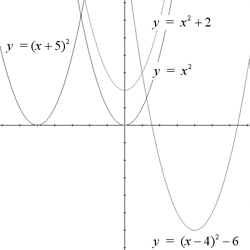
The vertex is the maximum point for
parabolas with a < 0 or minimum point for parabolas with a > 0.
For parabolas of the form y = ax2, the vertex is (0,0). The
vertex of a parabola can be shifted however, and this change is
reflected in the standard equation for parabolas. Given a parabola y=ax2+bx+c,
we can find the x-coordinate of the vertex of the parabola using the
formula x=-b/2a. The standard equation
has the form y = a(x - h)2 + k. The parabola y = ax2
is shifted h units to the right and k units upwards, resulting in a
parabola with vertex (h,k).
Note: You may recognize
this equation from the completing the square section above. The method
of completing the square should be used to convert a parabola of
general form to its standard form.
Note: For an example of
graphing a quadratic equation, see question #2 in the Additional
Examples section below.
Additional Examples
1
| Solve the quadratic equation by completing the square
2
| Solve and graph the quadratic equation by completing the square
|
Top of Page |
|

