|
This tutorial exhibits some of the applications
of integral calculus. Although these are only some of the applications
of integration, they will give you an idea of how calculus can be used
to solve problems in other areas of mathematics.
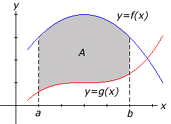
The area A of the region bounded by the curves,
f(x) and g(x), and the lines x=a and x=b, where f and g are continuous
and f(x)>g(x) for all x in the interval [a, b], is given by
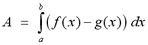
The figure to the right illustrates the region
that is given by the definition above. To make the image clearer, the
curve f(x) is shown in blue and the curve g(x) is shown in red.

In some problems, the curves may intersect so
that f(x) is not greater than g(x) over the entire interval [a, b]. The
graph to the right illustrates this situation. In this case, we must
find the point of intersection, c, between the two curves. To find the
point of intersection c, we set f(x) = g(x) and solve the resulting
equation for x. To find the area, we split the
region A between the curves into 2 separate regions, A1,
bounded by f(x) and g(x) and the lines x=a and x=c, and A2,
bounded by g(x) and f(x) and the lines x=c and x=b. To find the area of
A, we calculate the area of each individual region and take the sum of
the results.
For the curve to the right, the equation for the
area of the region would be given by
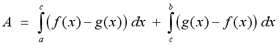
Note: This equation
depends on the nature of the question. Not all problems will use this
same equation to determine the area. For example, if the curve g(x) is
greater than f(x) on [a,c), and less than f(x) on (c,b], we would
switch the f(x) with g(x) in the equation above.
In other problems, the region may be bounded by
the curves f(x) and g(x) over part of the interval [a,b] but may be
bounded by only a single curve for another part of the interval. The
figure below illustrates this situation.
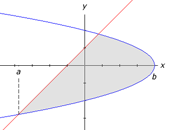
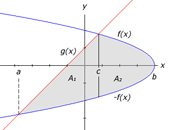
In a problem like this, there are two possible
solutions.
a) The first method is to find the point of
intersection, c, between the two curves. We split the region A between
the curves into 2 separate regions, A1, bounded by f(x) and
g(x) and the lines x=a and x=c, and A2, bounded by +f(x) and
-f(x) and the lines x=c and x=b. The image to the right illustrates the
first method of solving this type of area problem. The formula to the
below shows how the area would be calculated for this specific example.
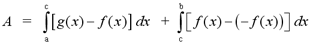
Note: Like the problem
above, this equation depends on the nature of the question. You must
recognize which function defines the upper boundary and which defines
the lowers boundary over a certain interval.
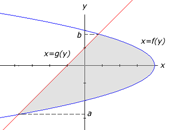
b) The second method involves rewriting the
problem so that it is in terms of y rather than x. We express each
curve in terms of y, so that we have f(y) for the right boundary and
g(y) for the left boundary. We must find the y coordinates of the
intersection points of the curves. We let y=b represent the higher
intersection point and y=a represent the lower intersection point. The
image to the right illustrates the second approach to solving the
example above. The equation below shows how the area would be
calculated for this specific example.
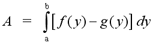
Note: Once again, this
equation depends on the nature of the question.
In fact, this method can be used to solve any
area problems. It may often be simpler to solve the integrals when the
functions in terms of y rather than x. If the problem seems too
difficult, we can always try to solve it in terms of y.
Examples
1
| Find the area of the region between the curves
2
| Find the area of the region between the intersecting curves
3
| Find the area of the region between the curves, with respect to y
Integration also allows us to calculate the
volumes of solids. Let S be a solid that lies between x=a and x=b. Let
the continuous function A(x) represent the cross-sectional area of S in
the plane through the point x and perpendicular to the x-axis. The
volume of S is given by
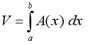
Now that we have the definition of volume, the
challenging part is to find the function of the area of a given cross
section. This process is quite similar to finding the area between
curves.
Most volume problems that we will encounter will
be require us to calculate the volume of a solid of rotation.
These are solids that are obtained when a region is rotated about some
line. A typical volume problem would ask, "Find the volume of the solid
obtained by rotating the region bounded by the curve(s) about some
specified line." Since the region is rotated about a specific line, the
solid obtained by this rotation will have a disk-shaped cross-section.
We know from simple geometry that the area of a circle is given by A = p r2. For each cross-sectional disk,
the radius is determined by the curves that bound the region. If we
sketch the region bounded by the given curves, we can easily find a
function to determine the radius of the cross-sectional disk at point x.
The figures above illustrates this concept. The
figure to the left shows the region bounded by the curve 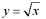 and the x-axis
and the lines x = 0 and x = 2. The figure in the center shows the
3-dimensional solid that is formed when the region from the first
figure is rotated about the x-axis. The figute to the right shows a
typical cross-sectional disk. A disk for a given value x between 0 and
2 will have a radius of and the x-axis
and the lines x = 0 and x = 2. The figure in the center shows the
3-dimensional solid that is formed when the region from the first
figure is rotated about the x-axis. The figute to the right shows a
typical cross-sectional disk. A disk for a given value x between 0 and
2 will have a radius of 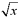 . The area of the disk is given by A(x) = p ( . The area of the disk is given by A(x) = p (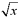 )2 or equivalently, A(x) = px. Once we find the area function, we simply
integrate from a to b to find the volume. The examples below will show
complete solutions to finding the area of a given solid. )2 or equivalently, A(x) = px. Once we find the area function, we simply
integrate from a to b to find the volume. The examples below will show
complete solutions to finding the area of a given solid.
Variations of Volume Problems
There are several variations in these types of
problems. The first factor that can vary in a volume problem is the
axis of rotation. What if the region from the figure above was rotated
about the y-axis rather than the x-axis? We would end up with a
different function for the radius of a cross-sectional disk. The
function would be written with respect to y rather than x, so we would
have to integrate with respect to y. In general, we can use the
following rule.
If the region bounded by the curves f(x) and g(x)
and the lines x=a and x=b is rotated about an axis parallel to the
x-axis, write the integral with respect to x. If the axis of rotation
is parallel to the y-axis, write the integral with respect to y.
The second factor that can vary in volume
problems is the radius of a typical cross-sectional disk. Suppose that
the region is bounded by two curves, f(x) and g(x), that both vary
between x=a and x=b. The solid that is created by rotating this region
about some specified line will have a hole in the center. The radius of
a cross-sectional disk will be determined by two functions, rather than
a single function. This variation creates two separate styles of
problems.

The Disk Method : The disk method is used
when the cross sections are disk shaped. The radius of a cross section
is determined by a single function, f(x). The area of the disk is given
by the formula, A(x) = p (radius)2.
The figure to the right shows a typical cross-sectional disk.
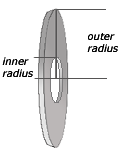
The Washer Method : The washer method is
used when the cross sections are washer shaped. The radius of a cross
section is determined by a two functions, f(x) and g(x). This gives us
two separate radii, an outer radius, from f(x) to the axis of rotation
and an inner radius from g(x) to the axis of rotation. The area of the
washer is given by the formula, A(x) = p [
(outer radius)2-(inner radius)2 ]. The figure to
the left shows a typical cross-sectional washer.
Examples
4
| Find the volume of the solid (axis of rotation parallel to y-axis)
5
| Find the volume of the solid using the washer method
There is another method to solve volume problems,
in addition to the methods described in the section above. The method
of cylindrical shells is sometimes simpler to use than the previous
methods. For example, suppose we want to find the volume of the solid
obtained by rotating about the y-axis, the region bounded by the y=3x-x3
and the line y=0. Since the axis of rotation is parallel to the y-axis,
we must integrate the area function with respect to y. To do this, We
must solve the cubic function for x in terms of y. This would be rather
difficult. However, we will soon see that this problem can be solved
quite easily using the method of cylindrical shells.
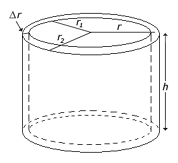
The image to the right shows a cylindrical shell
with outer radius r2, inner radius r1 and height
h. We can calculate the volume of the shell by finding the volume of
the inner cylinder, V1 and subtracting it from the volume of
the outer cylinder, V2. Recall from the geometry tutorial,
that the volume of a cylinder is given by the formula V = pi r2h.
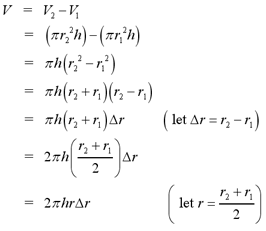
We let 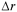 represent the thickness of
the cylindrical shell and r represent the average radius of the shell.
In summary, the volume of a cylindrical shell is given by the following
formula represent the thickness of
the cylindrical shell and r represent the average radius of the shell.
In summary, the volume of a cylindrical shell is given by the following
formula
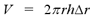
Now that we have covered the concept of a
cylindrical shell, we can apply it to general volume problems. The idea
behind the method of cylindrical shells is to think of a 3-dimensional
solid as a collection of cylindrical shells. To find the volume of the
solid, we must integrate the formula for the volume of a cylindrical
shell. However, the formula for the volume of the cylindrical shell
will vary with each problem. We must find functions for the height and
the radius of the cylindrical shell at x. Suppose the functions are
h(x) for height and r(x) for radius. The volume of the solid obtained
by rotating a region about a specific line from a to b is given by
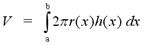
This may seem complicated, but after a few
examples the method will be much clearer.
Examples
6
| Find the volume of the solid using the method of cylindrical shells
7
| Find the volume of the solid
For more practice with the concepts covered in
this tutorial, visit the Area and Volume Problems page
at the link below.
The solutions to the problems will be posted after these chapters are
covered in your calculus course.
To test your knowledge of applications of integration problems, try
taking the
general area and volume test on the iLrn website or the
advanced
area and volume test at the link below.
Area & Volume
Problems
General Area & Volume Test on iLrn
Advanced Area &
Volume Test
|Top
of Page |
|

