|
A polynomial is a sum of one or more
terms, where each term consists of a constant and one or more variables
raised to some non-negative integer exponents. A polynomial with only
one term is
called a monomial, two terms, a binomial and three
terms, a trinomial. Some examples of each type are listed below.
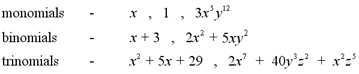
The degree of an individual term in a
polynomial is the sum of the exponents of the variables in that term.
For example, the term x2y3 has a degree of 5,
since the exponents of the variables x and y ( 2 and 3 respectively )
add up to 5.
Note : This is one of
the laws of exponents, which will be covered in the exponents tutorial.
The degree of a polynomial is the largest
degree of any of its individual terms. The polynomial x2y3
+ xy3 + 5y would have a degree of 5, since that is the
largest degree of each of its terms.
A root of a polynomial p(x) is a number, a,
such that p(a)=0. If a is a root of a polynomial p(x),
then p can be factored such that p(x)=(x-a)q(x) for some polynomial
q(x). The different methods of factoring polynomials are found in the
section below.
Factoring Binomials
The simplest method of factoring binomials is to
remove factors that are common to different terms. This method does not
work in all situations. The formulas listed below can be used to factor
binomials that fit the specific situation.
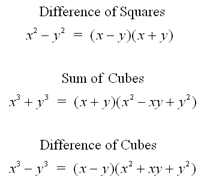
Examples
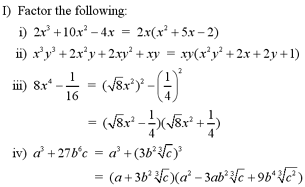
Factoring Trinomials
Quadratic trinomials have the form ax2
+ bx + c. When factoring these trinomials, we want to write them as a
product of two binomials. The two types of quadratic trinomials are
listed below.
Monic quadratic trinomials are
expressions where the leading coefficient (a) is equal to 1. For
example, x2 + 7x + 12 is a monic quadratic trinomial. These
trinomials are the simplest to factor. For the general monic quadratic
trinomial, x2 + bx + c, we must find the roots of the
polynomial, x1 and x2,
such that x2 + bx + c = (x-x1)(x-x2).
By expanding the factorization, we see that x2 + bx + c = x2
- (x1+x2)x + (x1x2). From
this expansion, we get the formulas b = -(x1+x2)
and c = x1x2. We can use these formulas to find
the roots of the polynomial, if it can be factored.
The simplest way to factor monic quadratic
trinomials is to look for integer roots. If we cannot find integer
roots however, it does not mean that the trinomial can't be factored.
We must use the quadratic formula, which is given in the quadratic
equations tutorial, to find the non-integer roots of the quadratic
trinomial. If no roots exist, however, then the trinomial cannot be
factored.
Examples
Nonmonic quadratic trinomials are
expressions where the leading coeffecient (a) is not equal to 1. For
example 6x2 - 11x - 7 is a nonmonic quadratic trinomial. To
factor these trinomials, we must again find roots x1 and x2
such that ax2+bx+c = a(x - x1)(x - x2).
The simplest way to factor a nonmonic trinomial
is to find two integers m and n, such that m
+ n = b and m x n = ac. After finding the two integers, substitute the
bx term for the sum of terms mx + nx. Then remove common factors. If no
integers can be found, it does not necessarily mean that the polynomial
cannot be factored. We must find the non-integer roots of the
polynomial using the quadratic formula. If there are no roots of the
polynomial, it cannot be factored.
Examples
Note: For an example of
factoring a polynomial using grouping, see question #1 in the
Additional Examples section at the
bottom of the page.
The Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra states
: Any polynomial with real coefficients can be split into the product
of linear or quadratic factors.
However, although the linear or quadratic factors
are polynomials, they may not be able to be split any further. For
example, the quadratic equation y = x2 + x + 1 cannot be
split any further.
Note: The complete
Fundamental Theorem of Algebra contains references to complex numbers
which is more complicated of a theorem than is required for the scope
of the first year calculus course. The theorem in its place above is a
simplified version. More information on the Fundamental Theorem of
Algebra can be found in any first year algebra textbook.
Rational Expressions
A rational expression is a quotient
where the numerator and the denominator are both polynomials. The rules
for operations of fractions can also be applied to operations involving
rational expressions.
Examples
Note: For a more
complex example of performing arithmetic operations with rational
expressions, see question #2 in the Additional Examples section below.
Additional Examples
1
| Example of a polynomial factored using grouping
2
| Example of operations performed on rational expressions
|
Top of Page |
|

