Before continuing with the inverse functions tutorial, it's recommended that you review the exponents, logarithms and trigonometry tutorials at the links below.

Inverse Functions

To fully understand the concept of an inverse function, we must first review the concept of a one-to-one function in the glossary.

Suppose f is a one-to-one function with domain X and range Y. The inverse function f ^-1 has domain Y and range X and is defined by

for any y in Y.

The images below illustrate the concept of an inverse function.

Note: The notation for an inverse function, f ^-1 is often mistaken with an exponenetial expression. To express the reciprocal 1/f(x), we would write [f(x)]^-1.

Cancellation Equations

The composition of inverse functions yields some very interesting results. The following equations are known as cancellation equations for inverse functions.

Steps for Finding Inverse Functions

If we are given the formula for a function f(x), how do we find the formula for the inverse function f ^-1? The steps below describe the process to determine the inverse of a function.

1) Write the formula for the function, y=f(x).

2) If possible, solve the equation for x in terms of y.

3) Interchange the variables x and y, so that the inverse is a function of x. We end up with the function, y = f ^-1(x).

Inverse Functions and Calculus

There are two theorems that relate the inverse functions to concepts covered in previous calculus tutorials. The first theorem deals with the continuity of inverse functions.

If f is a one-to-one function and is continuous on an interval I, then it inverse function, f ^-1 is continuous on f(I).

Note: This is due to the fact that the domain of the inverse function f ^-1 is the range of f, as explained above.

The next theorem gives us a formula to calculate the derivative of an inverse function.

If f is a one-to-one, differentiable function with inverse, g=f ^-1 and f'(g(a)) does not equal 0, then the inverse function is differentiable at a and

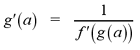
Examples

The Definition of e

Recall the irrational number e from the logarithm tutorial. When we first introduced this number, we did not have the knowledge of calculus to properly define it.

The irrational number e is a number such that

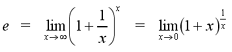
From the definition of e, it can be shown that

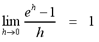
Graph of the Natural Exponential Function

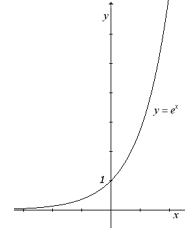
The function f(x) = e^x is known as the natural exponential function. The graph to the right shows the natural exponential function. We can see that the function is increasing and continuous for all values of x in R. The domain is X = {x | x is in R) and the range is Y = {y | y > 0}.

The graph also illustrates the functions behaviour as x approaches positive and negative infinity.

The natural exponential function has a horizontal asymptote at y = 0.

The Derivative and Integral of the Natural Exponential Function

The natural exponential function has a very simple derivative.

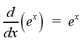
If we combine the formula above with the chain rule, the formula becomes

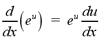
Since the derivative of the exponential function is so simple, it is very easy to calculate the integral.

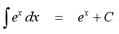
Examples

Limits of Logarithmic Functions

We can apply the concepts of calculus to logarithmic functions, so that we can better understand them. In order to graph logarithmic functions, we will need to know how they behave at infinity and at the vertical asymptote x = 0. If a > 1, then

Similarly, the following limits indicate the behaviour of the natural logarithmic function as x approaches infinity and as x approaches 0.

Note: Recall that logarithmic functions and the natural logaritmic function are not defined for x less than or equal to 0.

Derivatives of Logarithmic and Exponential Functions

Recall the natural logarithmic function, y = ln x. Since The derivative of the natural logarithmic function is given by the formula below.

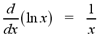
If we combine the formula above with the chain rule, the formula becomes

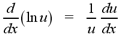
The integral that corresponds with the derivative of the natural logarithmic function, shown above, is given by the formula below.

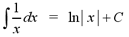
From the derivative of the natural logarithmic function, we get the formula for the derivative of regular logarithimic functions.

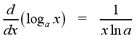
From the derivatives of the natural exponential and natural logarithmic functions, we have a formula for the derivative of exponential functions with base a. These functions have the form a^x

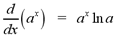
The integral of an exponential function with base a is given by the following formula

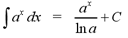
Note: Be careful not to confuse the exponential function a^x with the function x^a. The function, a^x has a variable exponent and constant base. When differentiating, we use the formula above. The function x^a has a constant exponent and variable base. When differentiating, we simply use the power rule.

The formulas above are very important to remember. Since there are so many and they are so similar, students often get confused between the different formulas. In your textbook, there are full derivations of each formula. Many of these derivations are simple enough that students can simply derive the formula on a test or exam. It may be helpful to look over these derivations if you find it difficult to memorize the formulas.

Examples

Logarithmic Differentiation

The process of logarithmic differentiation allows us to calculate the derivatives of complicated functions. For example, the function y = x^x cannot be differentiated using any of the methods we have covered thus far. The steps of logarithmic differentiation are outlined below.

1) Given an equation y = f(x), take the logarithm of each side and simplify the equation using the properties of logarithms.

2) Use the method of implicit differentiation to differentiate the simplified equation, with respect to x.

3) Solve the equation for y'

Although this method of differentiation may seem complicated, it will be much clearer after a few examples.

Examples

Inverse Trigonometric Functions

This section combines the idea of inverse functions with trigonometric functions. However, for a function to have an inverse function, it must be one-to-one. Although trigonometric functions are not one-to-one, (try applying the horizontal line test to y = sin x, for example), we can restrict the domain so that they become one-to-one functions.

Recall the graph of the sine function from the trigonometry tutorial. If we restrict the domain of the function to -pi/2 < x < pi/2, the function becomes one-to-one. The inverse of this function exists and is called the inverse sine function, denoted sin^-1 or the arcsine function, denoted arcsin. These two notations are used interchangeably.

The definition of the inverse sine function is shown below.

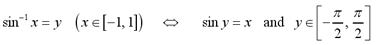
The graphs of the sine function and the corresponding inverse sine function are shown below.

Since the arcsine and sine functions are inverse functions, we can apply the cancellation equations. The cancellation equations are shown below.

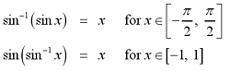
Note: When using any of the trigonometric cancellation equations, we must be sure that x lies in the specified interval. If it does not, we cannot apply the cancellation equation and must find some alternate approach to solve the problem.

We can also relate the concept of an inverse trigonometric function with calculus. The inverse sine function, sin^-1 with domain [-1, 1] and range [-pi/2, pi/2] is continuous. The derivative of the inverse sine function is given by the formula below.

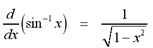
From the differentiation formula, we also have a formula for integration that involves the inverse sine function.

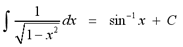
The inverse cosine function is defined quite similarly to the inverse sine function. The domain of the cosine function is restricted to [0, pi], so that the it becomes a one-to-one function. The definition of the arccosine function is shown below.

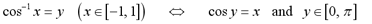
The graphs of the cosine function and the corresponding inverse cosine function are shown below.

The canellation equations become

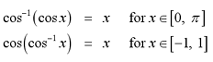
The inverse cosine function, cos^-1 with domain [-1, 1] and range [0, pi] is continuous. The derivative of the inverse cosine function is given by the formula below.

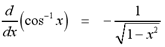
From the differentiation formula, we also have a formula for integration that involves the inverse cosine function.

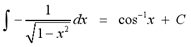
Note: The integral above could also be evaluated to -sin^-1 x + C. By convetnion, we calculate all variations of the integral above to be equal to the inverse sine function. The inverse cosine function is still correct, but it is preferred that you express the integral as the inverse sine function.

The inverse tangent function is also similar to the previously defined inverse trigonometric functions. The domain of the tangent function is restricted to [-pi/2, pi/2], so that it becomes a one-to-one function. The definition of the arctangent function is shown below.

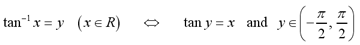
The graphs of the tangent function and the corresponding inverse tangent function are shown below.

The canellation equations become

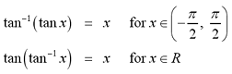
The inverse tangent function, tan^-1 with domain, R and range (-pi/2, pi/2) is continuous. The derivative of the inverse tangent function is given by the formula below.

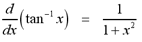
From the differentiation formula, we also have a formula for integration that involves the inverse tangent function.

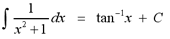
Although the remaining trigonometric functions exist, they are not used as frequently as the three defined above. The table below summarizes the definitions of all inverse trigonometric functions.

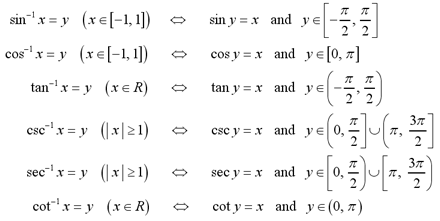
The following table summarizes the differentiation formulas for all inverse trigonometric functions.

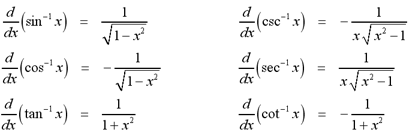
In addition to the integration formulas above, there are a few other useful integration formulas that involve the inverse trigonometric functions.

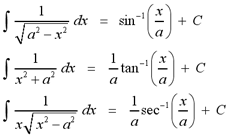
Examples

For more practice with the concepts covered in this tutorial, visit the Inverse Functions Problems page at the link below. The solutions to the problems will be posted after these chapters are covered in your calculus course.

To test your knowledge of inverse function problems, try taking the general inverse functions test on the iLrn website or the advanced inverse functions test at the link below.

|Top of Page |