Inequalities
Inequalities are statements of the form:
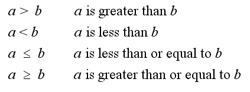
The following are a set of properties for
inequalities:
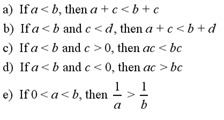
The solution set of an inequality is the
set of numbers for which the inequality is true. Two inequalities are equivalent
if they have the same solution sets.
Examples
Note: For examples of
graphing an inequality, see questions #2 and #3 in Additional Examples
at the bottom of
the page.
Absolute Value
The absolute value of a real number x can
be thought of as the distance from 0 to x on the real number line.
Absolute value, denoted |x|, is defined as follows:
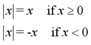
Note: Absolute value,
|x| is always nonnegative, since it is a distance on the real number
line.
Properties
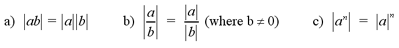
Examples
Absolute Value & Inequalities
The properties listed below describe how to solve
inequalities that contain absolute values.
Properties
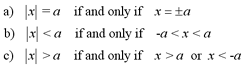
Examples
Note: For a more
complex example of solving an absolute inequality, see question #1 in
the Additional Examples section below.
Additional Examples
1
| Solve the inequality
2
| Graph the region determined by the inequality
3
| Graph the region determined by the parabolic inequality
|
Top of Page |
|

