Calculus Applications
Calculus is a very versatile and valuable tool. It is a form
of mathematics which was developed from algebra and geometry. It is made
up of two interconnected topics, differential calculus and integral calculus.
You can look at differential calculus as the mathematics of
motion and change. Integral calculus covers the accumulation of quantities, such as
areas under a curve. The two ideas work inversely together as defined by the
Fundamental Theorem of Calculus.
Calculus is deeply integrated in every branch of the physical sciences, such as
physics and biology. It is found in computer science, statistics, and engineering;
in economics, business, and medicine. Modern developments such as architecture,
aviation, and other technologies all make use of what calculus can offer. This page
is designed to out line some of the applications of calculus and give you some idea
of why calculus is so important and useful.
Finding the Slope of a Curve
Calculus can give us a generalized method of finding the slope of a curve. The slope
of a line is fairly elementary, using some basic algebra it can be found. Although
when we are dealing with a curve it is a different story. Calculus allows us to find
out how steeply a curve will tilt at any given time. This can be very useful in any
area of study.
Calculating the Area of Any Shape
Although we do have standard methods to calculate the area of some shapes, calculus
allows us to do much more. Trying to find the area on a shape like this would
be very difficult if it wasn’t for calculus.
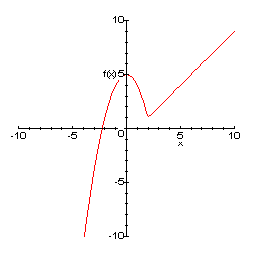Calculate Complicated X-intercepts
Without an idea like the Intermediate Value Theorem it would be exceptionally hard to
find or even know that a root existed in some functions. Using Newton’s Method you can
also calculate an irrational root to any degree of accuracy, something your calculator
would not be able to tell you if it wasn’t for calculus.
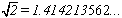
Visualizing Graphs
Using calculus you can practically graph any function or equation you would like. In
fact you can find out the maximum and minimum values, where it increases and decreases
and much more without even graphing a point, all using calculus.
 Finding the Average of a Function
A function can represent many things. One example is the path of an airplane. Using
calculus you can calculate its average cruising altitude, velocity and acceleration.
Same goes for a car, bus, or anything else that moves along a path. Now what would you
do without a speedometer on your car?
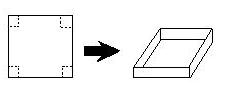Calculating Optimal Values
By using the optimization of functions in just a few steps you can answer very practical
and useful questions such as: “You have square piece of cardboard, with sides 1 meter in
length. Using that piece of card board, you can make a box, what are the dimensions of a
box containing the maximal volume?” These types of problems are a wonderful result of what
calculus can do for us.
Calculus is one of the greatest inventions of modern science. There is just so much it
can offer. The success of calculus has been extended over time into various other
important topics in mathematics. Some are: differential equations, vector calculus,
calculus of variations, complex analysis and differential topology. Studying calculus
gives you the fundamentals you will need in all of your future studies. Enjoy!
|Top
of Page |
|
